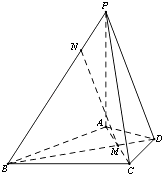
题目内容
【题目】已知函数![]() ,
,![]() 为
为![]() 的导数.
的导数.
(1)讨论函数![]() 的零点个数;
的零点个数;
(2)若函数![]() 的定义域内不单调且在
的定义域内不单调且在![]() 上单调递减,求实数
上单调递减,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析 (2)![]()
【解析】试题分析:
(1)原问题等价于函数![]() 和
和![]() 图象的交点的个数,分类讨论可得:
图象的交点的个数,分类讨论可得:![]() 时,
时,![]() 无零点;
无零点;![]() 或
或![]() 时,
时,![]() 有一个零点;
有一个零点;![]() 时,
时,![]() 有两个零点.
有两个零点.
(2)结合(1)的结论,利用导函数列表分类讨论函数的单调性可得实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(1)![]() ,
,
令![]() 得
得![]() 即
即![]() ,所以函数
,所以函数![]() 的零点个数等价于两函数
的零点个数等价于两函数![]() 和
和![]() 图象的交点的个数,
图象的交点的个数,
设两者相切时切点为![]() ,则由
,则由![]() 且
且![]() ,
,
得![]() .
.
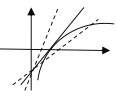
由图可知![]() 时,两函数图象无交点,
时,两函数图象无交点,![]() 无零点;
无零点;
![]() 时,两函数图象有两个交点,
时,两函数图象有两个交点,![]() 有两个零点.
有两个零点.
解法二:![]() ,
,
令![]() 得
得![]() 即
即![]() ,所以
,所以![]() ,所以函数
,所以函数![]() 的零点个数等价于两函数
的零点个数等价于两函数![]() 与
与![]() 的交点个数.
的交点个数.
因为![]() ,
,
所以![]() 时,
时,![]() ,
,![]() 递增;
递增;![]() 时,
时,![]() ,
,![]() 递减且
递减且![]() ,
,
![]() 时,
时,![]() 有极大值
有极大值![]() ,
,

如图所示,由图可知,两函数图象无交点,![]() 无零点;
无零点;
![]() 或
或![]() 时,两函数图象有一个交点,
时,两函数图象有一个交点,![]() 有一个零点;
有一个零点;
![]() 时,两函数图象有两个交点,
时,两函数图象有两个交点,![]() 有两个零点.
有两个零点.
解法三:直接由![]() 的导函数判断原函数的单调性及零点,因为函数取正值或负值时的特殊值不易找,请谨慎处理,如果仅仅交代单调性而不说明零点存在定理的条件(即
的导函数判断原函数的单调性及零点,因为函数取正值或负值时的特殊值不易找,请谨慎处理,如果仅仅交代单调性而不说明零点存在定理的条件(即![]() )中的
)中的![]() 的、或者只用限说明的,要酌情扣分。
的、或者只用限说明的,要酌情扣分。
(2)解法1:由(1)知![]() 时,
时,![]() 无零点或一个零点,
无零点或一个零点,![]() ,函数
,函数![]() 在定义域内单调递减,函数
在定义域内单调递减,函数![]() 在定义域内不单调时,
在定义域内不单调时,![]() .
.
![]() 在
在![]() 上单调递减时,
上单调递减时,![]() ,即
,即![]() ,亦等价于
,亦等价于![]() 时,
时,![]() ,
,
![]() .
.
①当![]() 时,
时,![]() ,
,![]() 递增,
递增,![]() 不合题意;
不合题意;
②当![]() 时,
时,![]() ,此时
,此时![]() ,
,![]() 递减,
递减,
![]() 时,
时,![]() ,由
,由![]() 得
得![]() ,解得
,解得![]() ,
,
所以![]() ;
;
③当![]() 时,
时,![]() ,
,![]() 时,由表可知
时,由表可知![]() 时,
时,![]() 取最大值,最大值为
取最大值,最大值为![]() ,不合题意.
,不合题意.
|
|
|
|
| 正 | 0 | 负 |
| 增 | 极大值 | 减 |
综上可知![]() .
.
解法二:由(1)知![]() 时,
时,![]() 无零点或一个零点,
无零点或一个零点,![]() ,函数
,函数![]() 在定义域内单调递减,函数
在定义域内单调递减,函数![]() 在定义域内不单调时,
在定义域内不单调时,![]() .
.
![]() 在
在![]() 上单调递减时,
上单调递减时,![]() ,即
,即![]() 恒成立;
恒成立;
由![]() 得
得![]() ,令
,令![]() ,则
,则![]() 恒成立,
恒成立,
因为![]() ,所以
,所以![]() 时
时![]() ,
,![]() 单调递减,
单调递减,
![]() ,由
,由![]() 恒成立得
恒成立得![]() ,解得
,解得![]() .
.
综上可得![]() .
.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案【题目】长春市的“名师云课”活动自开展以来获得广大家长和学子的高度赞誉,在我市推出的第二季名师云课中,数学学科共计推出36节云课,为了更好地将课程内容呈现给广大学子,现对某一时段云课的点击量进行统计:
点击量 |
|
|
|
节数 | 6 | 18 | 12 |
(Ⅰ)现从36节云课中采用分层抽样的方式选出6节,求选出的点击量超过3000的节数.
(Ⅱ)为了更好地搭建云课平台,现将云课进行剪辑,若点击量在区间![]() 内,则需要花费40分钟进行剪辑,若点击量在区间
内,则需要花费40分钟进行剪辑,若点击量在区间![]() 内,则需要花费20分钟进行剪辑,点击量超过3000,则不需要剪辑,现从(Ⅰ)中选出的6节课中任意取出2节课进行剪辑,求剪辑时间为40分钟的概率.
内,则需要花费20分钟进行剪辑,点击量超过3000,则不需要剪辑,现从(Ⅰ)中选出的6节课中任意取出2节课进行剪辑,求剪辑时间为40分钟的概率.