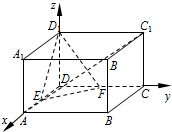
题目内容
在长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=a,E,F分别为AD,CD的中点.
(1)若AC1⊥D1F,求a的值;
(2)若a=2,求二面角E-FD1-D的余弦值.

(1)若AC1⊥D1F,求a的值;
(2)若a=2,求二面角E-FD1-D的余弦值.

(1)如图,以D为坐标原点,DA所在直线为x轴,
DC所在直线为y轴,DD1所在直线为z轴,建立坐标系.
∵AB=AD=2,AA1=a,E,F分别为AD,CD的中点,
∴A(2,0,0),D1(0,0,a),
C1(0,2,a),F(0,1,0).
∴
=(-2,2,a),
=(0,1,-a).…(2分)
∵AC1⊥D1F,∴
•
=0,即(-2,2,a)•(0,1,-a)=0.
∴2-a2=0,又a>0,解得a=
.…(5分)
(2)平面FD1D的一个法向量为
=(1,0,0).
设平面EFD1的一个法向量为
=(x,y,z),
∵E(1,0,0),a=2,
∴
=(-1,1,0),
=(0,1,-2).
由
⊥
,
⊥
,得-x+y=0且y-2z=0,
解得x=y=2z.
故平面EFD1的一个法向量为
=(2,2,1).…(8分)
∵cos<
,
>=
=
=
,
且二面角E-FD1-D的大小为锐角,
∴二面角E-FD1-D的余弦值为
.…(10分)
DC所在直线为y轴,DD1所在直线为z轴,建立坐标系.
∵AB=AD=2,AA1=a,E,F分别为AD,CD的中点,
∴A(2,0,0),D1(0,0,a),
C1(0,2,a),F(0,1,0).
∴
| AC1 |
| D1F |
∵AC1⊥D1F,∴
| AC1 |
| D1F |
∴2-a2=0,又a>0,解得a=
| 2 |
(2)平面FD1D的一个法向量为
| m |
设平面EFD1的一个法向量为
| n |
∵E(1,0,0),a=2,
∴
| EF |
| D1F |
由
| n |
| EF |
| n |
| D1F |
解得x=y=2z.
故平面EFD1的一个法向量为
| n |
∵cos<
| m |
| n |
| ||||
|
|
=
| (1,0,0)•(2,2,1) |
| 1×3 |
| 2 |
| 3 |
且二面角E-FD1-D的大小为锐角,
∴二面角E-FD1-D的余弦值为
| 2 |
| 3 |


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目




 =
=
 ,用
,用 ,
, 表示
表示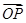 ,则
,则
