题目内容
已知双曲线的中心在原点，两个焦点为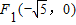
和
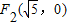，P在双曲线上，满足
且△F1PF2的面积为1，则此双曲线的方程是 ．
【答案】分析：设|PF1|=x，|PF2|=y，根据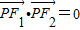
判断出∠PF1F2=90°进而根据三角形面积公式求得xy，最后根据勾股定理求得x2+y2的值，
进而求得y-x，根据双曲线定义求得a，最后根据a和c求得b，双曲线方程可得．
解答：解：设|PF1|=x，|PF2|=y，x＞y，
∵
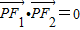
∴∠PF1F2=90°
∴
xy=1，xy=2
∵F1F1=2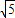
∴x2+y2=20
∴y-x=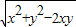
=4
∵y-x=2a=4
∴a=2
∴b=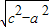
=1
∴双曲线方程为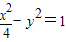
故答案为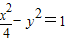
点评：本题主要考查了双曲线的标准方程．解题的关键是利用椭圆的定义求得a．
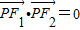判断出∠PF1F2=90°进而根据三角形面积公式求得xy，最后根据勾股定理求得x2+y2的值，进而求得y-x，根据双曲线定义求得a，最后根据a和c求得b，双曲线方程可得．
解答：解：设|PF1|=x，|PF2|=y，x＞y，
∵
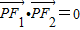
∴∠PF1F2=90°
∴
xy=1，xy=2∵F1F1=2
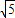
∴x2+y2=20
∴y-x=
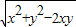=4∵y-x=2a=4
∴a=2
∴b=
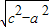=1∴双曲线方程为
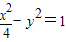
故答案为
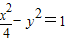
点评：本题主要考查了双曲线的标准方程．解题的关键是利用椭圆的定义求得a．
练习册系列答案
阅读快车系列答案
相关题目