题目内容
sin(x+30°)cos(x-30°)-cos(x+30°)sin(x-30°)=( )A.

B.

C.sin2
D.cos2
【答案】分析:利用两角差的正弦公式把要求的式子化为 sin[(x+30°)-(x-30°)],运算求得结果.
解答:解:sin(x+30°)cos(x-30°)-cos(x+30°)sin(x-30°)=sin[(x+30°)-(x-30°)]
=sin60°=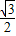 ,
,
故选B.
点评:本题主要考查两角差的正弦公式的应用,注意逆用公式,属于中档题.
解答:解:sin(x+30°)cos(x-30°)-cos(x+30°)sin(x-30°)=sin[(x+30°)-(x-30°)]
=sin60°=
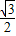 ,
,故选B.
点评:本题主要考查两角差的正弦公式的应用,注意逆用公式,属于中档题.

练习册系列答案
相关题目
下列说法错误的是( )
| A、如果命题“¬p”与命题“p或q”都是真命题,那么命题q一定是真命题; | ||
| B、命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0”; | ||
| C、若命题p:?x∈R,x2-x+1<0,则?p:?x∈R,x2-x+1≥0; | ||
D、“sinθ=
|