题目内容
已知函数
，
（Ⅰ）求函数
的最大值和最小正周期；
（Ⅱ）设
的内角
的对边分别
且
,
，若
求
的值．
（Ⅰ）0，
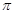（Ⅱ）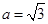
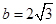
解析
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
培优口算题卡系列答案开心口算题卡系列答案口算题卡河北少年儿童出版社系列答案题目内容
已知函数，
（Ⅰ）求函数的最大值和最小正周期；
（Ⅱ）设的内角的对边分别且,，若求的值．
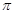（Ⅰ）0，（Ⅱ）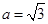
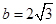
解析
培优口算题卡系列答案开心口算题卡系列答案口算题卡河北少年儿童出版社系列答案
, 
, 函数f(x)= 
的单调增区间。
的面积
满足
，且
，
与
的夹角为
.
的最大值及最小值． 
，设
（Ⅰ）求函数
的内角
的对边分别为
，已知
，求边
的值．
，
，
在
上的单调递增区间；
时，
恒成立，求实数
的取值范围. 
，
的最大值和最小正周期；
的内角
的对边分别
且
,
,若
求
的值．
的顶点在坐标原点，始边与x轴的非负半轴重合，终边经过点P
．
的值； K^S*5U.C
图象的对称中心为
，求
的值．
，且与向量
的夹角为
，其中
是
的内角． 
的大小； （2）求
的取值范围.
在长度为一个周期的闭
R）的图象经过怎样的变换得到。