题目内容
(本小题满分 分)
分)
设函数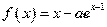 .
.
(Ⅰ)求函数 单调区间;
单调区间;
(Ⅱ)若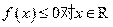 恒成立,求
恒成立,求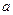 的取值范围;
的取值范围;
解:(I)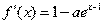
当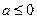 时,
时,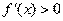 ,
,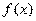 在
在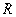 上是增函数;
上是增函数;
当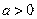 时,令
时,令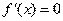 得
得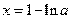 , ……………………3分
, ……………………3分
若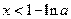 ,则
,则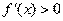 ,从而
,从而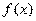 在区间
在区间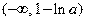 上是增函数;
上是增函数;
若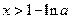 ,则
,则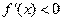 ,从而
,从而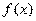 在区间
在区间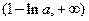 上是减函数.
上是减函数.
综上可知:当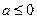 时,
时,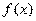 在区间
在区间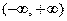 上是增函数.当
上是增函数.当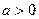 时,在区间
时,在区间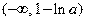 上是增函数,
上是增函数,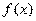 在区间
在区间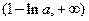 上是减函数 …………6分
上是减函数 …………6分
(II)由(I)可知:当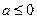 时,
时,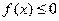 不恒成立 …………8分
不恒成立 …………8分
又当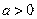 时,
时,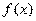 在点
在点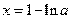 处取最大值,
处取最大值,
且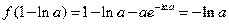 ………………10分
………………10分
令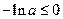 得
得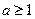
故若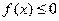 对
对 恒成立,则
恒成立,则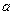 的取值范围是
的取值范围是 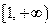 ……12分
……12分
解析

练习册系列答案
相关题目
 的部分图象如图所示:
的部分图象如图所示: 的值;
的值; ,当
,当 时,求函数
时,求函数 的值域.
的值域.
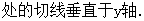
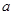 分别表示
分别表示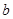 和
和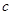 ;
;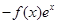 的单调区间。
的单调区间。