题目内容
如图,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC,设点F为棱AD的中点.
(1)求证:DC⊥平面ABC;
(2)求直线BF与平面ACD所成角的余弦值.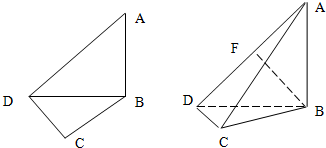
(1)求证:DC⊥平面ABC;
(2)求直线BF与平面ACD所成角的余弦值.

(本小题满分14分)
(1)证明:在图甲中∵AB=BD,且∠A=45°,
∴∠ADB=45°,∠ABD=90°,
即AB⊥BD,
在图乙中,∵平面ABD⊥平面BDC,且平面ABD∩平面BDC=BD
∴AB⊥底面BDC,∴AB⊥CD.
又∠DCB=90°,∴DC⊥BC,且AB∩BC=B,
∴DC⊥平面ABC. …(7分)
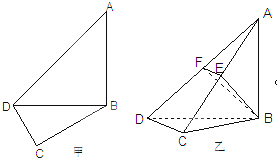
(2)作BE⊥AC,垂足为E.
由(1)知平面ABC⊥平面ACD,又平面ABC∩平面ACD=AC,∴BF⊥平面ADC,
∴∠AFE即为直线BF与平面ACD所成角
设CD=a,得AB=BD=2a,BC=
| 3 |
| 7 |
∴BE=
2
| ||
|
| 2 |
| 2 | ||
|
∴cos∠BFE=
| ||||
|
| ||
| 7 |
∴直线BF与平面ACD所成角的余弦值为
| ||
| 7 |

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
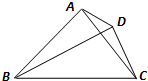 如图,在平面四边形ABCD中,若AB=2,CD=1,则
如图,在平面四边形ABCD中,若AB=2,CD=1,则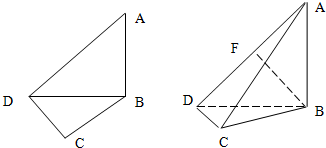 如图,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC,设点F为棱AD的中点.
如图,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC,设点F为棱AD的中点.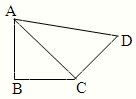 如图,在平面四边形ABCD中,AB=BC=CD=a,∠ABC=90°,∠BCD=135°,沿对角线AC将此四边形折成直二面角.
如图,在平面四边形ABCD中,AB=BC=CD=a,∠ABC=90°,∠BCD=135°,沿对角线AC将此四边形折成直二面角.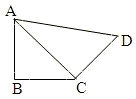 如图,在平面四边形ABCD中,AB=BC=CD=a,∠ABC=90°,∠BCD=135°,沿对角线AC将此四边形折成直二面角.
如图,在平面四边形ABCD中,AB=BC=CD=a,∠ABC=90°,∠BCD=135°,沿对角线AC将此四边形折成直二面角.