题目内容
【题目】2017年10月份郑州市进行了高三学生的体育学业水平测试,为了考察高中学生的身体素质比情况,现抽取了某校1000名(男生800名,女生200名)学生的测试成绩,根据性别按分层抽样的方法抽取100名进行分析,得到如下统计图表:
男生测试情况:
抽样情况 | 病残免试 | 不合格 | 合格 | 良好 | 优秀 |
人数 | 5 | 10 | 15 | 47 |
|
女生测试情况
抽样情况 | 病残免试 | 不合格 | 合格 | 良好 | 优秀 |
人数 | 2 | 3 | 10 |
| 2 |
(1)现从抽取的1000名且测试等级为“优秀”的学生中随机选出两名学生,求选出的这两名学生恰好是一男一女的概率;
(2)若测试等级为“良好”或“优秀”的学生为“体育达人”,其它等级的学生(含病残免试)为“非体育达人”,根据以上统计数据填写下面列联表,并回答能否在犯错误的概率不超过0.010的前提下认为“是否为体育达人”与性别有关?
男性 | 女性 | 总计 | |
体育达人 | |||
非体育达人 | |||
总计 |
临界值表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
附:(  ,其中
,其中![]() )
)
【答案】(1)![]() (2)在犯错误的概率不超过0.010的前提下可以认为“是否为‘体育达人’与性别无关”
(2)在犯错误的概率不超过0.010的前提下可以认为“是否为‘体育达人’与性别无关”
【解析】试题分析: ![]() 按分层抽样男生应抽取
按分层抽样男生应抽取![]() 名,女生应抽取
名,女生应抽取![]() 名,从而得到
名,从而得到![]() ,
, ![]() ,从而得到
,从而得到![]() 名任意选
名任意选![]() 名总的基本事件,利用古典概型及其概率的计算公式,即可求解概率;
名总的基本事件,利用古典概型及其概率的计算公式,即可求解概率;
![]() 列出列联表,利用对立性检验的公式,求得
列出列联表,利用对立性检验的公式,求得![]() ,即可得到结论。
,即可得到结论。
解析:(1)按分层抽样男生应抽取80名,女生应抽取20名.
![]() ,
, ![]()
抽取的100名且测试等级为优秀的学生中有三位男生,设为![]() ,
, ![]() ,
, ![]() ;
;
两位女生设为![]() ,
, ![]() .从5名任意选2名,总的基本事件有
.从5名任意选2名,总的基本事件有![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,共10个.
,共10个.
设“选出的两名学生恰好是一男一女为事件![]() ”.
”.
则事件包含的基本事件有![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共6个.
共6个.
![]()
(2)![]() 列联表如下表:
列联表如下表:
男生 | 女生 | 总计 | |
体育达人 | 50 | 5 | 55 |
非体育达人 | 30 | 15 | 45 |
总计 | 80 | 20 | 100 |
则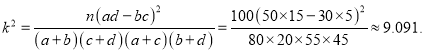
![]() 且
且![]() .
.
所以在犯错误的概率不超过0.010的前提下可以认为“是否为‘体育达人’与性别无关”.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案