题目内容
设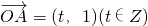 ,
,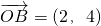 ,满足
,满足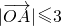 ,则当△OAB是直角三角形时t的值为________.
,则当△OAB是直角三角形时t的值为________.
-2或-1
分析:根据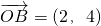 ,可求出OB=2
,可求出OB=2 >OA,根据△OAB是直角三角形,分类讨论,当∠AOB=90°时或当∠OBA=90°时,或∠OAB=90°,利用向量垂直的充要条件
>OA,根据△OAB是直角三角形,分类讨论,当∠AOB=90°时或当∠OBA=90°时,或∠OAB=90°,利用向量垂直的充要条件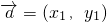 ,
,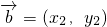 ,
, ?x1x2+y1y2=0,即可求得结果.
?x1x2+y1y2=0,即可求得结果.
解答:∵OB=2 >OA
>OA
∴1°当∠AOB=90°时,有2t+4=0,
解得t=-2,
2°当∠OBA=90°时,有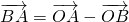 =(t-2,-3)
=(t-2,-3)
∴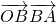 =2(t-2)-12=0,
=2(t-2)-12=0,
解得t=8,
因为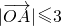 ,所以t=8,不满足题意,舍去,
,所以t=8,不满足题意,舍去,
3°当∠OAB=90°,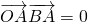 ,
,
t(t-2)-3=0,解得t=-1或t=3(舍去);
综上t=-2,或t=-1;
故答案为:-2或-1.
点评:本题考查利用向量的数量积判断两向量的垂直关系,注意向量垂直的充要条件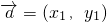 ,
,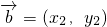
 ?x1x2+y1y2=0,和三角形是直角三角形要分类讨论,体现了分类讨论的思想,同时考查了运算能力,属中档题.
?x1x2+y1y2=0,和三角形是直角三角形要分类讨论,体现了分类讨论的思想,同时考查了运算能力,属中档题.
分析:根据
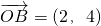 ,可求出OB=2
,可求出OB=2 >OA,根据△OAB是直角三角形,分类讨论,当∠AOB=90°时或当∠OBA=90°时,或∠OAB=90°,利用向量垂直的充要条件
>OA,根据△OAB是直角三角形,分类讨论,当∠AOB=90°时或当∠OBA=90°时,或∠OAB=90°,利用向量垂直的充要条件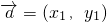 ,
,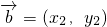 ,
, ?x1x2+y1y2=0,即可求得结果.
?x1x2+y1y2=0,即可求得结果.解答:∵OB=2
 >OA
>OA∴1°当∠AOB=90°时,有2t+4=0,
解得t=-2,
2°当∠OBA=90°时,有
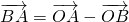 =(t-2,-3)
=(t-2,-3)∴
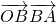 =2(t-2)-12=0,
=2(t-2)-12=0,解得t=8,
因为
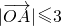 ,所以t=8,不满足题意,舍去,
,所以t=8,不满足题意,舍去,3°当∠OAB=90°,
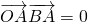 ,
,t(t-2)-3=0,解得t=-1或t=3(舍去);
综上t=-2,或t=-1;
故答案为:-2或-1.
点评:本题考查利用向量的数量积判断两向量的垂直关系,注意向量垂直的充要条件
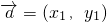 ,
,
 ?x1x2+y1y2=0,和三角形是直角三角形要分类讨论,体现了分类讨论的思想,同时考查了运算能力,属中档题.
?x1x2+y1y2=0,和三角形是直角三角形要分类讨论,体现了分类讨论的思想,同时考查了运算能力,属中档题. 
练习册系列答案
相关题目
设O为坐标原点,点M坐标为(3,2),若点N(x,y)满足不等式组:
,当3≤s≤5时,则
•
的最大值的变化范围是( )
|
| OM |
| ON |
| A、[7,8] |
| B、[7,9] |
| C、[6,8] |
| D、[7,15] |