题目内容
已知数列{an}的前n项和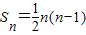 ,且an是bn与1的等差中项.
,且an是bn与1的等差中项.(1)求数列{an}和数列{bn}的通项公式;
(2)若
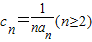 ,求c2+c3+c4+…+cn;
,求c2+c3+c4+…+cn;(3)若
 ,是否存在n∈N*使得f(n+11)=2f(n),并说明理由.
,是否存在n∈N*使得f(n+11)=2f(n),并说明理由.
【答案】分析:(1)当n大于等于2时,由an=Sn-Sn-1得出通项公式,然后把n=1代入通项公式进行验证,即可得到数列{an}的通项公式,再由an是bn与1的等差中项,根据等差数列的性质得到2an=bn+1,由数列{an}的通项公式即可求出数列{bn}的通项公式;
(2)把(1)得出的数列{an}的通项公式,代入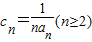 ,利用拆项的方法变形,然后列举出c2+c3+c4+…+cn的各项,抵消合并可求出值;
,利用拆项的方法变形,然后列举出c2+c3+c4+…+cn的各项,抵消合并可求出值;
(3)不存在,理由为:分n为奇数和偶数两种情况考虑:当n为奇数时,n+11为偶数,分别代入相应的解析式中求出f(n)和f(n+11),发现方程f(n+11)=2f(n)无解;当n为偶数时,n+11为奇数,分别代入相应的解析式中求出f(n)和f(n+11),发现方程f(n+11)=2f(n)也无解,故不存在n使f(n+11)=2f(n).
解答:解:(1)当n≥2时,an=Sn-Sn-1= n(n-1)-
n(n-1)- (n-1)(n-2)=n-1,
(n-1)(n-2)=n-1,
把n=1代入验证,满足通项公式,
则an=n-1,又an是bn与1的等差中项,
则bn=2an-1=2(n-1)-1=2n-3;
(2)因为an=n-1,
所以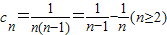 ,
,
则c2+c3+c4+…+cn=1- +
+ -
- +
+ -
- …+
…+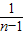 -
-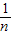 =1-
=1-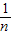 ;
;
(3)不存在,理由为:
当n是奇数时,n+11为偶数,
此时f(n)=an=n-1,f(n+11)=bn+11=2n+19,
由f(n+11)=2f(n)知无解;
当n是偶数时,n+11为奇数,
此时f(n)=bn=2n-3,f(n+11)=an+11=n+10,
由f(n+11)=2f(n)知无解,
所以满足题意的n不存在.
点评:此题考查了等差数列的通项公式,等差数列的性质,数列的求和,以及分类讨论思想的运用,熟练掌握等差数列的通项公式及性质是解本题的关键,其中注意第二小问拆项的方法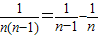 .
.
(2)把(1)得出的数列{an}的通项公式,代入
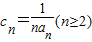 ,利用拆项的方法变形,然后列举出c2+c3+c4+…+cn的各项,抵消合并可求出值;
,利用拆项的方法变形,然后列举出c2+c3+c4+…+cn的各项,抵消合并可求出值;(3)不存在,理由为:分n为奇数和偶数两种情况考虑:当n为奇数时,n+11为偶数,分别代入相应的解析式中求出f(n)和f(n+11),发现方程f(n+11)=2f(n)无解;当n为偶数时,n+11为奇数,分别代入相应的解析式中求出f(n)和f(n+11),发现方程f(n+11)=2f(n)也无解,故不存在n使f(n+11)=2f(n).
解答:解:(1)当n≥2时,an=Sn-Sn-1=
 n(n-1)-
n(n-1)- (n-1)(n-2)=n-1,
(n-1)(n-2)=n-1,把n=1代入验证,满足通项公式,
则an=n-1,又an是bn与1的等差中项,
则bn=2an-1=2(n-1)-1=2n-3;
(2)因为an=n-1,
所以
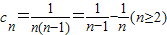 ,
,则c2+c3+c4+…+cn=1-
 +
+ -
- +
+ -
- …+
…+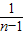 -
-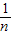 =1-
=1-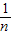 ;
;(3)不存在,理由为:
当n是奇数时,n+11为偶数,
此时f(n)=an=n-1,f(n+11)=bn+11=2n+19,
由f(n+11)=2f(n)知无解;
当n是偶数时,n+11为奇数,
此时f(n)=bn=2n-3,f(n+11)=an+11=n+10,
由f(n+11)=2f(n)知无解,
所以满足题意的n不存在.
点评:此题考查了等差数列的通项公式,等差数列的性质,数列的求和,以及分类讨论思想的运用,熟练掌握等差数列的通项公式及性质是解本题的关键,其中注意第二小问拆项的方法
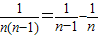 .
. 
练习册系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |