题目内容
已知a，b是实数，函数f(x)＝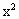
＋ax＋1，且y＝f(x＋1)在定义域上是偶函数，函数g(x)＝－bf[f(x＋1)]＋(3b－1)f(x＋1)＋2在区间(－∞，－2)上是减函数，且在区间(－2，0)上是增函数．
(Ⅰ)求a；
(Ⅱ)求b；
(Ⅲ)如果在区间(－∞，－1)上存在函数 F(x)，满足F(x)·f(x＋1)＝g(x)，当x为何值时，F(x)取得的最小值．
答案：
解析：
解析：
|
(1)∵f(x＋1)= ∴f(x＋1)=f(－x＋1)即 t∈[4，＋∞)；当x∈[－2，0)时t是x的减函数，且t∈(0，4)，又g(x)在(－∞，－2]减函数在(－2，0)上增函数，则h(t)=－b (3)由(2)及x∈(－∞，－1)得g(x)= |
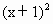＋a(x＋1)＋1是R上的偶函数，
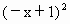＋a(－x＋1)＋1，∴4x＋2ax＝0，∴a=－2．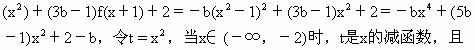
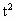＋(5b－1)t－b＋2，利用复合函数性质知h(t)在[4，＋∞)是增函数，在(0，4)上是减函数，由二次函数单调性有b＜0，且
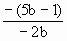=4，得b=
．
，则F(x)=
，当
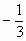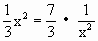时等号成立，又x∈(－∞，－1)，则当x=－
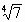时F(x)取最小值
．
练习册系列答案
华东师大版一课一练系列答案
相关题目
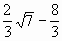=（x，1），
=（-1，b-x），函数f（x）=a-
是偶函数．
=（x，1），
=（-1，b-x），函数f（x）=a-
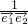是偶函数．