题目内容
(本小题满分12分)
已知函數f(x)=ln+mx2(m∈R)
(I)求函数f(x)的单调区间;
(II)若A,B是函数f(x)图象上不同的两点,且直线AB的斜率恒大于1,求实数m的取值范围。
【答案】
(Ⅰ)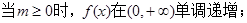
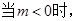
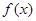 在
在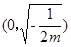 上单调递增,在
上单调递增,在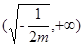 上单调递减.
上单调递减.
(Ⅱ) 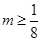 .
.
【解析】
试题分析:(Ⅰ)f(x)的定义域为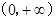 ,
, 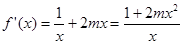 …………2分
…………2分
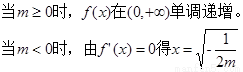
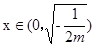 时,
时,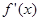 >0,
>0,
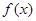 在
在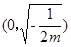 上单调递增;
上单调递增;
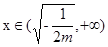 时,
时,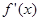 <0,
<0,
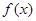 在
在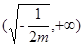 上单调递减.
上单调递减.
综上所述: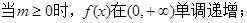
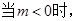
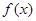 在
在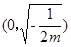 上单调递增,在
上单调递增,在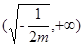 上单调递减.
上单调递减.
……………5分
(Ⅱ) 依题意,设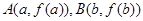 ,不妨设
,不妨设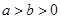 ,
,
则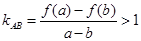 恒成立,…………6分
恒成立,…………6分
,则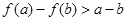 恒成立,
恒成立,
所以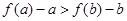 恒成立,
恒成立,
令 ……………8分
……………8分
则g(x)在 为增函数,
为增函数,
所以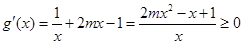 ,对
,对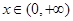 恒成立,…………10分
恒成立,…………10分
所以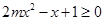 ,对
,对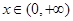 恒成立,
恒成立,
即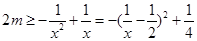 ,对
,对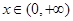 恒成立,
恒成立,
因此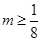 .……………12分
.……………12分
考点:本题主要考查应用导数研究函数的单调性及极值,二次函数的图象和性质。
点评:典型题,本题属于导数应用中的基本问题,(2)涉及恒成立问题,转化成求函数的最值,这种思路是一般解法,往往要利用“分离参数法”,本题最终化为二次函数最值问题,体现考题“起点高,落点低”的特点。涉及对数函数,要特别注意函数的定义域。

练习册系列答案
相关题目