题目内容
数列{an}满足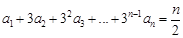 ,则
,则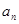 = .
= .

解析

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
在等差数列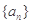 中,
中,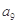 =
=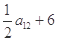 ,则数列
,则数列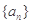 的前11项和
的前11项和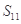 =( )
=( )
| A.24 | B.48 | C.66 | D.132 |
题目内容
数列{an}满足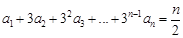 ,则
,则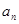 = .
= .

解析

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案在等差数列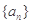 中,
中,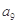 =
=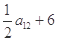 ,则数列
,则数列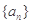 的前11项和
的前11项和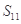 =( )
=( )
| A.24 | B.48 | C.66 | D.132 |