题目内容
已知数列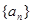 满足:
满足: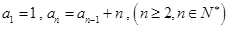 .
.
(Ⅰ)求数列的通项公式;
(Ⅱ)设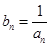 ,求数列
,求数列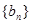 的前
的前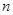 项和
项和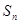 .
.
(Ⅰ)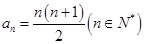 ;(Ⅱ)
;(Ⅱ)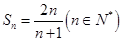 .
.
解析试题分析:(Ⅰ)由已知条件中给出的通项的递推公式,转变为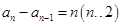 ,列出
,列出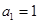 及
及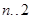 时各项式子,利用叠加消项法求数列
时各项式子,利用叠加消项法求数列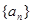 的通项公式(叠加消项法在求数列的通项、前
的通项公式(叠加消项法在求数列的通项、前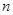 项和中常常用到,其特点是根据等式两边结构特征,一边相加可消掉中间项,另一边相加可以得到某一特殊数列或是常数);(Ⅱ)由(Ⅰ)结果知数列
项和中常常用到,其特点是根据等式两边结构特征,一边相加可消掉中间项,另一边相加可以得到某一特殊数列或是常数);(Ⅱ)由(Ⅰ)结果知数列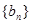 的通项为
的通项为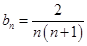 ,观察其通项公式特点
,观察其通项公式特点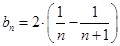 ,可采用裂项相消法来求其前
,可采用裂项相消法来求其前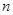 项和
项和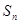 (裂项相消法在求前
(裂项相消法在求前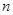 项和中常用的一种方法,其特点是通项公式可裂开成两项之差,相加后可以消掉中间项).
项和中常用的一种方法,其特点是通项公式可裂开成两项之差,相加后可以消掉中间项).
试题解析:(Ⅰ)由已知得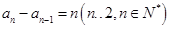 ,
,
所以有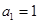 ,
,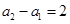 ,
,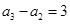 , ,
, ,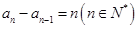
将上述等式叠加可得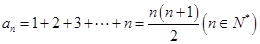
当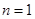 时满足上式,所以所求数列
时满足上式,所以所求数列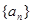 的通项公式为
的通项公式为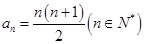 . 6分
. 6分
(Ⅱ)由(Ⅰ)知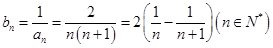 , 9分
, 9分
所以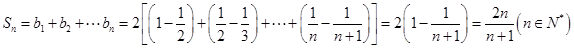 12分
12分
考点:1.数列通项(叠加消项法);2.数列前 项和(裂项相消法)
项和(裂项相消法) (裂项相消法).
(裂项相消法).

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
设等差数列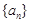 的公差d不为0,
的公差d不为0,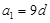 ,若
,若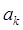 是
是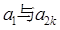 的等比中项,则k=( )
的等比中项,则k=( )
| A.2 | B.6 | C.8 | D.4 |
在等差数列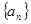 中,若
中,若 ,则
,则 ( )
( )
| A.45 | B.75 | C.180 | D.300 |

 的前
的前 项和
项和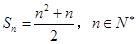 .
.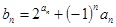 ,求数列
,求数列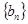 的前
的前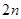 项和.
项和.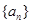 的前
的前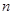 项和为
项和为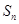 ,且
,且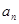 是
是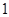 的等差中项,等差数列
的等差中项,等差数列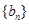 满足
满足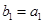 ,
,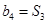 .
.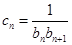 ,数列
,数列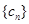 的前
的前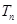 ,证明:
,证明: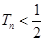 .
. 的前
的前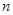 项和
项和 ,数列
,数列 满足
满足
 .
. ;(Ⅱ)求数列
;(Ⅱ)求数列 ;
; ,求数列
,求数列 的前
的前 .
.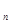 }满足0<a
}满足0<a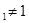 , 且
, 且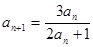 (n
(n N*).
N*). 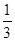 ,求出a2、a3、a4、a5的值,归纳出an , 并用数学归纳法证明.
,求出a2、a3、a4、a5的值,归纳出an , 并用数学归纳法证明.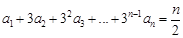 ,则
,则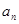 = .
= .