题目内容
设a<c<b,如果把函数y=f(x)的图象被两条平行的直线x=a,x=b所截的一段近似地看作一条线段,则下列关系式中,f(c)的最佳近似表示式是( )
A、f(c)=
| ||
B、f(c)=
| ||
C、f(c)=f(a)+
| ||
D、f(c)=f(a)-
|
分析:由题意可得A(a,f(a)),B(b,f(b)),则过点A,B的直线方程为:
=
,把x=c代入可求
| y-f(a) |
| f(b)-f(a) |
| x-a |
| b-a |
解答:解:由题意可得A(a,f(a)),B(b,f(b))
则过点A,B的直线方程为:
=
从而可得,f(c)=
[f(b)-f(a)]+f(a)
故选C.
则过点A,B的直线方程为:
| y-f(a) |
| f(b)-f(a) |
| x-a |
| b-a |
从而可得,f(c)=
| c-a |
| b-a |
故选C.
点评:本题主要考查了直线方程的两点式,解题的关键是利用两点式
=
,属于基础试题.
| y-y1 |
| y2-y1 |
| x-x1 |
| x2-x1 |

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
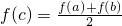
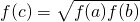
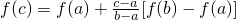
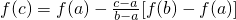
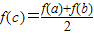
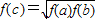
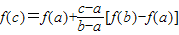
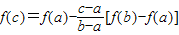
 [f(a)+f(b)]
[f(a)+f(b)]
 [f(b)-f(a)]
[f(b)-f(a)]