题目内容
(1)已知x>0,y>0,求证
≥
;(2)已知a、b是正数,求证
+
>a.
| x2 |
| x+y |
| 3x-y |
| 4 |
| a2 |
| b |
| b2 |
| a |
分析:(1)根据 x>0,y>0,
-
=
=
≥0,从而得到
≥
成立.
2)由于 a、b是正数,可得(a-b)2(a+b)≥0,即 a3+b3-a2b-ab2≥0,移项两边同时除以ab 可得
+
≥a+b>a.
| x2 |
| x+y |
| 3x-y |
| 4 |
| 4x2-(x+y)(3x-y) |
| 4(x+y) |
| (x-y)2 |
| 4(x+y) |
| x2 |
| x+y |
| 3x-y |
| 4 |
2)由于 a、b是正数,可得(a-b)2(a+b)≥0,即 a3+b3-a2b-ab2≥0,移项两边同时除以ab 可得
| a2 |
| b |
| b2 |
| a |
解答:证明:(1)∵x>0,y>0,
-
=
=
≥0,
∴
≥
成立.
证明:(2)∵a、b是正数,∴(a-b)2(a+b)≥0,∴a3+b3-a2b-ab2≥0,
∴a3+b3≥a2b+ab2,两边同时除以ab 可得
+
≥a+b>a,故
+
>a 成立.
| x2 |
| x+y |
| 3x-y |
| 4 |
| 4x2-(x+y)(3x-y) |
| 4(x+y) |
| (x-y)2 |
| 4(x+y) |
∴
| x2 |
| x+y |
| 3x-y |
| 4 |
证明:(2)∵a、b是正数,∴(a-b)2(a+b)≥0,∴a3+b3-a2b-ab2≥0,
∴a3+b3≥a2b+ab2,两边同时除以ab 可得
| a2 |
| b |
| b2 |
| a |
| a2 |
| b |
| b2 |
| a |
点评:本题主要考查用比较法和综合法证明不等式,注意这两种方法间的关系是互逆的,属于中档题.

练习册系列答案
相关题目
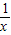 +
+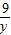 =2,求x+y的最小值.
=2,求x+y的最小值.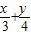 =1,求xy的最大值.
=1,求xy的最大值.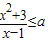 恒成立,求a的取值范围.
恒成立,求a的取值范围.