题目内容
(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分4分,第3小题满分8分。
已知双曲线C的中心是原点,右焦点为F![]() ,一条渐近线m:
,一条渐近线m:![]() ,设过点A
,设过点A![]() 的直线l的方向向量
的直线l的方向向量![]() 。
。
(1)求双曲线C的方程;
(2)若过原点的直线![]() ,且a与l的距离为
,且a与l的距离为![]() ,求K的值;
,求K的值;
(3)证明:当![]() 时,在双曲线C的右支上不存在点Q,使之到直线l的距离为
时,在双曲线C的右支上不存在点Q,使之到直线l的距离为![]() 。
。
(1)![]()
(2)![]()
(3)证明见解析。
解析:
(1)设双曲线![]() 的方程为
的方程为![]() ,
,
![]() ,解得
,解得![]() ,双曲线
,双曲线![]() 的方程为
的方程为![]() 。
。
(2)直线![]() ,直线
,直线![]() ,
,
由题意,得![]() ,解得
,解得![]() 。
。
(3)证法一:设过原点且平行于![]() 的直线
的直线![]() ,
,
则直线![]() 与
与![]() 的距离
的距离![]() ,当
,当![]() 时,
时,![]() ,
,
又双曲线![]() 的渐近线为
的渐近线为![]()
![]() ,
,
![]() 双曲线
双曲线![]() 的右支在直线
的右支在直线![]() 的右下方,
的右下方,
![]() 双曲线
双曲线![]() 右支上的任意点到直线
右支上的任意点到直线![]() 的距离大于
的距离大于![]() 。
。
故在双曲线![]() 的右支上不存在点
的右支上不存在点![]() ,使之到直线
,使之到直线![]() 的距离为
的距离为![]() 。
。
证法二:假设双曲线![]() 右支上存在点
右支上存在点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
则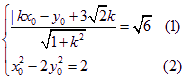
由(1)得![]()
设![]() ,
,
当![]() 时,
时,![]() ;
;
![]()
将![]() 代入(2)得
代入(2)得![]()
![]() ,
,
![]()
![]() 方程
方程![]() 不存在正根,即假设不成立,
不存在正根,即假设不成立,
故在双曲线![]() 的右支上不存在点
的右支上不存在点![]() ,使之到直线
,使之到直线![]() 的距离为
的距离为![]() 。
。

练习册系列答案
相关题目
 为偶函数, 且
为偶函数, 且
 的值;
的值; 为三角形
为三角形 的一个内角,求满足
的一个内角,求满足 的
的 为偶函数, 且
为偶函数, 且
 的值;
的值; 为三角形
为三角形 的一个内角,求满足
的一个内角,求满足 的
的