题目内容
已知直线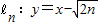
与圆Cn：x2+y2=2an+n+2（n∈N+）交于不同点An、Bn，其中数列an满足：
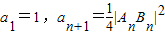．（Ⅰ）求数列an的通项公式；
（Ⅱ）设
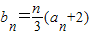，求数列bn的前n项和Sn．
【答案】分析：（I）由题意及数列{an}的已知的递推关系，求出该数列的通项公式；
（II）有数列{bn}的定义，在（I）的条件下是这一数列具体化，有通项公式选择错位相减法求出新数列的前n项和．
解答：解：（1）
∴
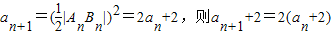
∴易得an=3×2n-1-2
（2）
，
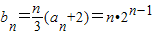Sn=1×2+2×21+3×22++n×2n-1
2Sn=1×21+2×22+3×23++n×2n
相减得Sn=（n-1）2n+1
点评：此题重点考查了有数列{an}的递推关系式，求其通项公式，还考查了利用错位相减法求数列{bn}的前n项和．
（II）有数列{bn}的定义，在（I）的条件下是这一数列具体化，有通项公式选择错位相减法求出新数列的前n项和．
解答：解：（1）
∴
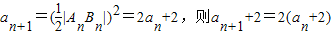
∴易得an=3×2n-1-2
（2）
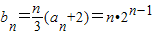，Sn=1×2+2×21+3×22++n×2n-1
2Sn=1×21+2×22+3×23++n×2n
相减得Sn=（n-1）2n+1
点评：此题重点考查了有数列{an}的递推关系式，求其通项公式，还考查了利用错位相减法求数列{bn}的前n项和．
练习册系列答案
阅读快车系列答案
相关题目
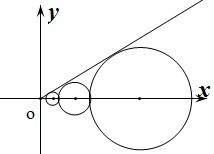
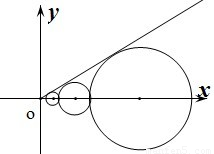
设C1，C2，…，Cn，…是坐标平面上的一列圆，它们的圆心都在x轴的正半轴上，且都与直线
与圆Cn：x2＋y2＝2an＋n＋2(n∈N+)交于不同点An、Bn，其中数列{an}满足：
求数列{bn}的前n项和Sn．
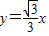相切，对每一个正整数n，圆Cn都与圆Cn+1相互外切，以rn表示Cn的半径，已知{rn}为递增数列．
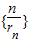的前n项和．