题目内容
(本小题满分12分)数列![]() 的通项是关于
的通项是关于![]() 的不等式
的不等式![]() 的解集中整数的个数,
的解集中整数的个数,![]() (1)求数列
(1)求数列![]() 的通项公式; (2)是否存在实数
的通项公式; (2)是否存在实数![]() 使不等式
使不等式![]() 对一切大于1的自然数
对一切大于1的自然数![]() 恒成立,若存在试确定
恒成立,若存在试确定![]() 的取值范围,否则说明原因.
的取值范围,否则说明原因.
(1) ![]() (2) 存在实数
(2) 存在实数![]() 且取值范围是
且取值范围是![]()
解析:
(1)不等式![]() 同解于(Ⅰ)
同解于(Ⅰ)![]() 或(Ⅱ)
或(Ⅱ)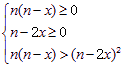
![]()
由(Ⅰ)解得 ;由(Ⅱ)解得
;由(Ⅱ)解得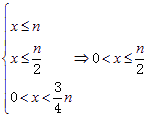
于是原不等式的解集为![]() .因此,
.因此,![]()
(2)假设存在实数![]() 使
使![]() 对于
对于![]() 的自然数恒成立.
的自然数恒成立.
由于![]()
![]() 则
则
![]() 两式相减得:
两式相减得:
![]()
∴![]() 当
当![]() ≥2且
≥2且![]() 是增函数∴
是增函数∴![]() 的最小值是
的最小值是![]()
若假设成立,则有![]()
∴![]() 或
或![]() 解得:
解得:![]() .
.
∴存在实数![]() 且取值范围是
且取值范围是![]()

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目