题目内容
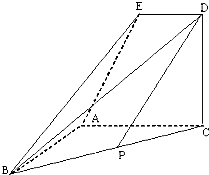 (2013•东城区一模)如图,已知ACDE是直角梯形,且ED∥AC,平面ACDE⊥平面ABC,∠BAC=∠ACD=90°,AB=AC=AE=2,ED=
(2013•东城区一模)如图,已知ACDE是直角梯形,且ED∥AC,平面ACDE⊥平面ABC,∠BAC=∠ACD=90°,AB=AC=AE=2,ED=| 1 | 2 |
(Ⅰ)求证:DP∥平面EAB;
(Ⅱ)求平面EBD与平面ABC所成锐二面角大小的余弦值.
分析:(I)取AB的中点F,连接PF,EF.利用三角形的中位线定理可得FP
AC.再利用已知条件和平行四边形的判定定理可得四边形EFPD是平行四边形,可得PD∥EF.利用线面平行的判定定理即可得出;
(II)通过建立空间直角坐标系,利用两个平面的法向量的夹角即可得出二面角.
| ∥ |
. |
| 1 |
| 2 |
(II)通过建立空间直角坐标系,利用两个平面的法向量的夹角即可得出二面角.
解答:(I)证明:取AB的中点F,连接PF,EF.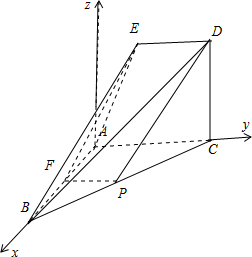
又∵P是BC的中点,∴FP
AC.
∵ED=
AB=
AC,ED∥AC,
∴FP
ED,
∴四边形EFPD是平行四边形,
∴PD∥EF.
而EF?平面EAB,PD?平面EAB,
∴PD∥平面EAB.
(II)∵∠BAC=90°,平面ACDE⊥平面ABC,∴BA⊥平面ACDE.
以点A为坐标原点,直线AB为x轴,AC为y轴,建立如图所示的空间直角坐标系,
则z轴在平面EACD内.则A(0,0,),B(2,0,0),E(0,1,
),D(0,2,
).
∴
=(2,-1,-
),
=(0,1,0).
设平面EBD的法向量
=(x,y,z),由
,得
,
取z=2,则x=
,y=0.∴
=(
,0,2).
可取
=(0,0,1)作为平面ABC的一个法向量,
∴cos<
,
>=
=
=
.
即平面EBD与平面ABC所成锐二面角大小的余弦值为
.

又∵P是BC的中点,∴FP
| ∥ |
. |
| 1 |
| 2 |
∵ED=
| 1 |
| 2 |
| 1 |
| 2 |
∴FP
| ∥ |
. |
∴四边形EFPD是平行四边形,
∴PD∥EF.
而EF?平面EAB,PD?平面EAB,
∴PD∥平面EAB.
(II)∵∠BAC=90°,平面ACDE⊥平面ABC,∴BA⊥平面ACDE.
以点A为坐标原点,直线AB为x轴,AC为y轴,建立如图所示的空间直角坐标系,
则z轴在平面EACD内.则A(0,0,),B(2,0,0),E(0,1,
| 3 |
| 3 |
∴
| EB |
| 3 |
| ED |
设平面EBD的法向量
| n |
|
|
取z=2,则x=
| 3 |
| n |
| 3 |
可取
| m |
∴cos<
| m |
| n |
| ||||
|
|
| 2 | ||
|
2
| ||
| 7 |
即平面EBD与平面ABC所成锐二面角大小的余弦值为
2
| ||
| 7 |
点评:熟练掌握三角形的中位线定理、平行四边形的判定和性质定理、线面平行的判定定理、面面垂直的性质定理、通过建立空间直角坐标系并利用两个平面的法向量的夹角得出二面角等是解题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 (2013•东城区一模)数列{an}的各项排成如图所示的三角形形状,其中每一行比上一行增加两项,若
(2013•东城区一模)数列{an}的各项排成如图所示的三角形形状,其中每一行比上一行增加两项,若