题目内容

已知P是椭圆
x2
100
+
y2
84
=1上的点，Q、R分别是圆（x+4）2+y2=1和圆（x-4）2+y2=1 上的点，则|PQ|+|PR|的最小值是（　　）
分析：设椭圆左右焦点为F1、F2，可得F1、F2恰好是两圆的圆心，有|PF1|+|PF2|=20，根据三角形两边之差小于第三边知：|PQ|最小为|PF1|-1，|PR|最小为|PF2|-1，由此即可求得|PQ|+|PR|的最小值．
解答：解：设椭圆左右焦点为F1、F2，可得F1（-4，0），F2（4，0）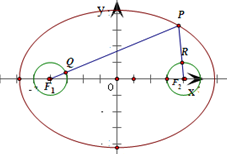
∴椭圆左右焦点恰好分别为两圆的圆心，且|PF1|+|PF2|=2a=20
由三角形两边之差小于第三边，
可知|PQ|的最小值为|PF1|-1，|PR|的最小值为|PF2|-1
∴|PQ|+|PR|≥|PF1|-1+|PF2|-1=20-2=18
故选：C
点评：本题给出椭圆上的点P、圆（x+4）2+y2=1上的点Q和圆（x-4）2+y2=1上的点R，求|PQ|+|PR|的最小值．着重考查了椭圆的定义与标准方程、圆的方程等知识，属于中档题．
练习册系列答案
相关题目
下列五个命题，其中真命题的序号是
 
（写出所有真命题的序号）．
（1）已知C：
x2
2-m
+
y2
m2-4
=1（m∈R），当m＜-2时C表示椭圆．
（2）在椭圆
x2
45
+
y2
20
=1上有一点P，F1、F2是椭圆的左，右焦点，△F1PF2为直角三角形则这样的点P有8个．
（3）曲线
x2
10-m
+
y2
6-m
=1(m＜6)与曲线
x2
5-m
+
y2
9-m
=1(5＜m＜9)的焦距相同．
（4）渐近线方程为y=±
b
a
x(a＞0，b＞0)的双曲线的标准方程一定是
x2
a2
-
y2
b2
=1
（5）抛物线y=ax2的焦点坐标为(0，
1
4a
)．
已知FΘ，FΡ是椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点，A，B分别是此椭圆的右顶点和上顶点，P是椭圆上一点，OP∥AB，PFΘ⊥x轴，|FΘA|=
10
+
5
，则此椭圆的方程是
x2
10
+
y2
5
=1
x2
10
+
y2
5
=1
．
下列五个命题，其中真命题的序号是______（写出所有真命题的序号）．
（1）已知C：
x2
2-m
+
y2
m2-4
=1（m∈R），当m＜-2时C表示椭圆．
（2）在椭圆
x2
45
+
y2
20
=1上有一点P，F1、F2是椭圆的左，右焦点，△F1PF2为直角三角形则这样的点P有8个．
（3）曲线
x2
10-m
+
y2
6-m
=1(m＜6)与曲线
x2
5-m
+
y2
9-m
=1(5＜m＜9)的焦距相同．
（4）渐近线方程为y=±
b
a
x(a＞0，b＞0)的双曲线的标准方程一定是
x2
a2
-
y2
b2
=1
（5）抛物线y=ax2的焦点坐标为(0，
1
4a
)．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网