题目内容
下列五个命题,其中真命题的序号是(1)已知C:
| x2 |
| 2-m |
| y2 |
| m2-4 |
(2)在椭圆
| x2 |
| 45 |
| y2 |
| 20 |
(3)曲线
| x2 |
| 10-m |
| y2 |
| 6-m |
| x2 |
| 5-m |
| y2 |
| 9-m |
(4)渐近线方程为y=±
| b |
| a |
| x2 |
| a2 |
| y2 |
| b2 |
(5)抛物线y=ax2的焦点坐标为(0,
| 1 |
| 4a |
分析:(1)先根据椭圆方程中2-m不等于m2-4即可得出答案.
(2)由条件知,以F1F2为直径的圆与椭圆有交点,故有圆的半径大于或等于短半轴的长度.结合圆与椭圆的位置关系求得答案.
(3)分别求得曲线
+
=1(m<6)与曲线
+
=1(5<m<9)的焦距即可;
(4)根据题意,近线方程为y=±
x(a>0,b>0)的双曲线的标准方程一定是
-
=λ(λ≠0);
(4)先把抛物线方程整理成标准方程,进而根据抛物线的性质可得焦点坐标.
(2)由条件知,以F1F2为直径的圆与椭圆有交点,故有圆的半径大于或等于短半轴的长度.结合圆与椭圆的位置关系求得答案.
(3)分别求得曲线
| x2 |
| 10-m |
| y2 |
| 6-m |
| x2 |
| 5-m |
| y2 |
| 9-m |
(4)根据题意,近线方程为y=±
| b |
| a |
| x2 |
| a2 |
| y2 |
| b2 |
(4)先把抛物线方程整理成标准方程,进而根据抛物线的性质可得焦点坐标.
解答:解:(1)当m=-3时,椭圆的方程变为C:
+
=1表示一个圆,故错;
(2)F1、F2是椭圆
+
=1(a>b>0)的焦点,P是椭圆上一点,且∠F1PF2=90°,
∴以F1F2为直径的圆与椭圆有交点,圆的半径r=c≥b,
∴圆与椭圆最多有4个交点,∴,△F1PF2为直角三角形则这样的点P最多有4个.故错;
(3)曲线
+
=1(m<6)与曲线
+
=1(5<m<9)的焦距都为4,相同,故正确;
(4)根据题意,近线方程为y=±
x(a>0,b>0)的双曲线的标准方程一定是
-
=λ(λ≠0)故错;
(5)整理抛物线方程得x2=
y,p=
∴焦点坐标为 (0,
)故正确.
故答案为:(3)(5)
| x2 |
| 5 |
| y2 |
| 5 |
(2)F1、F2是椭圆
| x2 |
| a2 |
| y2 |
| b2 |
∴以F1F2为直径的圆与椭圆有交点,圆的半径r=c≥b,
∴圆与椭圆最多有4个交点,∴,△F1PF2为直角三角形则这样的点P最多有4个.故错;
(3)曲线
| x2 |
| 10-m |
| y2 |
| 6-m |
| x2 |
| 5-m |
| y2 |
| 9-m |
(4)根据题意,近线方程为y=±
| b |
| a |
| x2 |
| a2 |
| y2 |
| b2 |
(5)整理抛物线方程得x2=
| 1 |
| a |
| 1 |
| 2a |
∴焦点坐标为 (0,
| 1 |
| 4a |
故答案为:(3)(5)
点评:本题考查圆锥曲线的共同特征、椭圆的标准方程和简单性质的应用.解决椭圆的标准方程的问题.要注意:对于椭圆标准方程
+
= 1,当焦点在x轴上时,a>b;当焦点在y轴上时,a<b.
| x2 |
| a2 |
| y2 |
| b2 |

练习册系列答案
相关题目
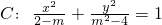 (m∈R),当m<-2时C表示椭圆.
(m∈R),当m<-2时C表示椭圆.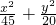 =1上有一点P,F1、F2是椭圆的左,右焦点,△F1PF2为直角三角形则这样的点P有8个.
=1上有一点P,F1、F2是椭圆的左,右焦点,△F1PF2为直角三角形则这样的点P有8个.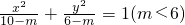 与曲线
与曲线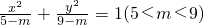 的焦距相同.
的焦距相同.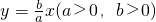 的双曲线的标准方程一定是
的双曲线的标准方程一定是
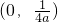 .
.