题目内容
已知FΘ,FΡ是椭圆
+
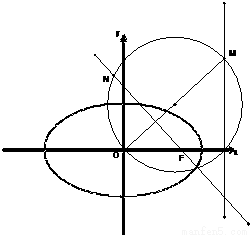
=1(a>b>0)的左、右焦点,A,B分别是此椭圆的右顶点和上顶点,P是椭圆上一点,OP∥AB,PFΘ⊥x轴,|FΘA|=
+
,则此椭圆的方程是
+
=1
+
=1.
| x2 |
| a2 |
| y2 |
| b2 |
| 10 |
| 5 |
| x2 |
| 10 |
| y2 |
| 5 |
| x2 |
| 10 |
| y2 |
| 5 |
分析:先把x=c代入椭圆方程求得y,进而求得|PF|,根据OP∥AB,PF∥OB推断出△PFO∽△ABO,进而根据相似三角形的性质求得
=
,求得b和c的关系,进而根据|FA|=
+
,则椭圆的方程可得.
| |PF| |
| |OF| |
| |OB| |
| |OA| |
| 10 |
| 5 |
解答: 解:把x=c代入椭圆方程求得y=±
解:把x=c代入椭圆方程求得y=±
,
∴|PF|=
,
∵OP∥AB,PF∥OB
∴△PFO∽△ABO
∴
=
,即
=
,求得b=c,
∴a=
c
∵|FA|=
+
,∴a+c=
+
,
∴a=
,b=c=
则此椭圆的方程是
+
=1
故答案为:
+
=1.
 解:把x=c代入椭圆方程求得y=±
解:把x=c代入椭圆方程求得y=±| b2 |
| a |
∴|PF|=
| b2 |
| a |
∵OP∥AB,PF∥OB
∴△PFO∽△ABO
∴
| |PF| |
| |OF| |
| |OB| |
| |OA| |
| ||
| c |
| b |
| a |
∴a=
| 2 |
∵|FA|=
| 10 |
| 5 |
| 10 |
| 5 |
∴a=
| 10 |
| 5 |
则此椭圆的方程是
| x2 |
| 10 |
| y2 |
| 5 |
故答案为:
| x2 |
| 10 |
| y2 |
| 5 |
点评:本题主要考查了椭圆的简单性质.考查了学生综合分析问题和基本的运算能力.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 已知椭圆
已知椭圆 +
+ =1经过点P(
=1经过点P( ,
, ),离心率是
),离心率是 ,动点M(2,t)(t>0)
,动点M(2,t)(t>0) ,F是椭圆
,F是椭圆 的右焦点,在椭圆上求一点M,使|AM|+2|MF|取得最小值.
的右焦点,在椭圆上求一点M,使|AM|+2|MF|取得最小值. +
+ =1经过点P(
=1经过点P(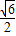 ,
, ),离心率是
),离心率是 ,动点M(2,t)(t>0)
,动点M(2,t)(t>0)
 +
+ =1经过点P(
=1经过点P(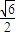 ,
, ),离心率是
),离心率是 ,动点M(2,t)(t>0)
,动点M(2,t)(t>0)