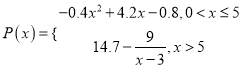题目内容
【题目】已知
，且
，求
（1）
的值；
（2）
的值.
【答案】（1）
；（2）
.
【解析】试题分析：（1）将条件平方得
，结合
，得sin θ>0，cos θ<0，进而sin θ－cos θ>0，求出(sinθ－cosθ)2开方即可；
（2）由①②得sin θ＋cos θ和sin θ－cos θ，求解sin θ和cos θ，即可得
.
试题解析：
（1）∵sin θ＋cos θ＝
，①∴(sin θ＋cos θ)2＝
，解得sin θcos θ＝－
.
∵0<θ<π，且sin θcos θ<0，∴sin θ>0，cos θ<0，∴sin θ－cos θ>0.
又∵(sinθ－cosθ)2=1－2sin θcos θ＝
∴sinθ-cosθ=
②.
（2）由①②得
sin θ＋cos θ＝
sin θ－cos θ＝.
解得sin θ＝
，cos θ＝－
∴tan θ＝
＝－
.
练习册系列答案
相关题目
