题目内容
1.根据正切函数的图象,写出使下列不等式成立的x的集合:(1)1+tanx≥0;
(2)tanx-$\sqrt{3}$≥0.
分析 (1)原不等式可化为tanx≥-1,由正切函数的图象和性质可得;
(2)原不等式可化为tanx≥$\sqrt{3}$,由正切函数的图象和性质可得.
解答  解:
解:
(1)由1+tanx≥0可得tanx≥-1,
∴由正切函数的性质可得kπ-$\frac{π}{4}$≤x<kπ+$\frac{π}{2}$,
∴使不等式成立的x的集合为{x|kπ-$\frac{π}{4}$≤x<kπ+$\frac{π}{2}$,k∈Z};
(2)由tanx-$\sqrt{3}$≥0可得tanx≥$\sqrt{3}$,
∴由正切函数的性质可得kπ+$\frac{π}{3}$≤x<kπ+$\frac{π}{2}$,
∴使不等式成立的x的集合为{x|kπ+$\frac{π}{3}$≤x<kπ+$\frac{π}{2}$,k∈Z}.
点评 本题考查正切函数的图象和性质,属基础题.

练习册系列答案
相关题目
11.从装有十个红球和十个白球的罐子里任取2球,下列情况中互斥而不对立的两个事件是( )
| A. | 至少有一个红球,至少有一个白球 | B. | 恰有一个红球,都是白球 | ||
| C. | 至少有一个红球,都是白球 | D. | 至多有一个红球,都是红球 |
9.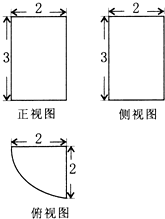 某空间几何体的三视图如图所示(其中俯视图的弧线为四分之一圆),则该几何体的表面积为( )
某空间几何体的三视图如图所示(其中俯视图的弧线为四分之一圆),则该几何体的表面积为( )
 某空间几何体的三视图如图所示(其中俯视图的弧线为四分之一圆),则该几何体的表面积为( )
某空间几何体的三视图如图所示(其中俯视图的弧线为四分之一圆),则该几何体的表面积为( )| A. | 5π+4 | B. | 14π+4 | C. | 5π+12 | D. | 14π+12 |