题目内容
m=-2是直线x+(m+1)y=2-m与f(x)=-| 1 |
| 6 |
| 1 |
| 2 |
分析:由题意得:f(x)在x=1处得切线斜率为:-
m2-
m,讨论当m=-1与m=2两种情况讨论直线x+(m+1)y=2-m的斜率,由两条直线的关系进而求出m的值.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:由题意得:f(x)的导数是f′(x)=-
m2x2-
m
所以f(x)在x=1处得切线斜率为:-
m2-
m
当m=-1时直线x+(m+1)y=2-m的斜率不存在,且切线的斜率为0,
此时两条直线相互垂直.
当m≠-1时直线x+(m+1)y=2-m的斜率为-
因为直线x+(m+1)y=2-m与f(x)=-
m2x3-
mx在x=1处的切线垂直
所以(-
)×(-
m2-
m)=-1
解得m=2
所以直线x+(m+1)y=2-m与f(x)=-
m2x3-
mx在x=1处的切线垂直时m=-1或m=2.
所以m=-2是直线x+(m+1)y=2-m与f(x)=-
m2x3-
mx在x=1处的切线垂直的充分不必要条件.
故答案为充分不必要条件.
| 1 |
| 2 |
| 1 |
| 2 |
所以f(x)在x=1处得切线斜率为:-
| 1 |
| 2 |
| 1 |
| 2 |
当m=-1时直线x+(m+1)y=2-m的斜率不存在,且切线的斜率为0,
此时两条直线相互垂直.
当m≠-1时直线x+(m+1)y=2-m的斜率为-
| 1 |
| m+1 |
因为直线x+(m+1)y=2-m与f(x)=-
| 1 |
| 6 |
| 1 |
| 2 |
所以(-
| 1 |
| m+1 |
| 1 |
| 2 |
| 1 |
| 2 |
解得m=2
所以直线x+(m+1)y=2-m与f(x)=-
| 1 |
| 6 |
| 1 |
| 2 |
所以m=-2是直线x+(m+1)y=2-m与f(x)=-
| 1 |
| 6 |
| 1 |
| 2 |
故答案为充分不必要条件.
点评:解决此类题目的关键是熟练利用导数求曲线的切线并且在表达直线的斜率时要注意斜率是否存在,这是直线这块常出错的地方.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
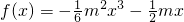 在x=1处的切线垂直的________条件.
在x=1处的切线垂直的________条件. 在x=1处的切线垂直的 条件.
在x=1处的切线垂直的 条件.