题目内容
从某批产品中,有放回地抽取产品二次,每次随机抽取1件,假设事件A:“取出的2件产品中至多有1件是二等品”的概率P(A)=0.96.
(Ⅰ)求从该批产品中任取1件是二等品的概率p;
(Ⅱ)若该批产品共100件,从中无放回抽取2件产品,ξ表示取出的2件产品中二等品的件数.求ξ的分布列.
(Ⅰ)求从该批产品中任取1件是二等品的概率p;
(Ⅱ)若该批产品共100件,从中无放回抽取2件产品,ξ表示取出的2件产品中二等品的件数.求ξ的分布列.
(Ⅰ)记A0表示事件“取出的2件产品中无二等品”,A1表示事件“取出的2件产品中恰有1件二等品”.
则A0,A1互斥,且A=A0+A1,故P(A)=P(A0+A1)=P(A0)+P(A1)=(1-p)2+
p(1-p)=1-p2
于是0.96=1-p2.解得p1=0.2,p2=-0.2(舍去).
(Ⅱ)ξ的可能取值为0,1,2.
若该批产品共100件,由(1)知其二等品有100×0.2=20件,故P(ξ=0)=
=
. P(ξ=1)=
=
. P(ξ=2)=
=
.
所以ξ的分布列为
则A0,A1互斥,且A=A0+A1,故P(A)=P(A0+A1)=P(A0)+P(A1)=(1-p)2+
| C | 12 |
于是0.96=1-p2.解得p1=0.2,p2=-0.2(舍去).
(Ⅱ)ξ的可能取值为0,1,2.
若该批产品共100件,由(1)知其二等品有100×0.2=20件,故P(ξ=0)=
| ||
|
| 316 |
| 495 |
| ||||
|
| 160 |
| 495 |
| ||
|
| 19 |
| 495 |
所以ξ的分布列为
| ξ | 0 | 1 | 2 | ||||||
| P |
|
|
|

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
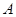 :“取出的2件产品都是二等品”的概率
:“取出的2件产品都是二等品”的概率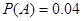
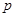 ;
;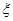 表示取出的2件产品中二等品的件数,求
表示取出的2件产品中二等品的件数,求