题目内容
从某批产品中,有放回地抽取产品二次,每次随机抽取1件,假设事件A:“取出的2件产品中至多有1件是二等品”的概率P(A)=0.96.(1)求从该批产品中任取1件是二等品的概率p;
(2)若该批产品共100件,从中任意抽取2件,求事件B:“取出的2件产品中至少有一件二等品”的概率P(B).
分析:(1)有放回地抽取产品二次,每次随机抽取1件,取出的2件产品中至多有1件是二等品包括无二等品和恰有一件是二等品两种情况,设出概率,列出等式,解出结果.
(2)由上面可以知道其中二等品有100×0.2=20件取出的2件产品中至少有一件二等品的对立事件是没有二等品,用组合数列出结果.
(2)由上面可以知道其中二等品有100×0.2=20件取出的2件产品中至少有一件二等品的对立事件是没有二等品,用组合数列出结果.
解答:解:(1)记A0表示事件“取出的2件产品中无二等品”,A1表示事件“取出的2件产品中恰有1件二等品”.
则A0,A1互斥,且A=A0+A1,故P(A)=P(A0+A1)
=P(A0)+P(A1)
=(1-p)2+C21p(1-p)
=1-p2
于是0.96=1-p2.
解得p1=0.2,p2=-0.2(舍去).
(2)记B0表示事件“取出的2件产品中无二等品”,
则B=
.
若该批产品共100件,由(1)知其中二等品有100×0.2=20件,故P(B0)=
=
.P(B)=P(
)=1-P(B0)=1-
=
则A0,A1互斥,且A=A0+A1,故P(A)=P(A0+A1)
=P(A0)+P(A1)
=(1-p)2+C21p(1-p)
=1-p2
于是0.96=1-p2.
解得p1=0.2,p2=-0.2(舍去).
(2)记B0表示事件“取出的2件产品中无二等品”,
则B=
. |
| B0 |
若该批产品共100件,由(1)知其中二等品有100×0.2=20件,故P(B0)=
| ||
|
| 316 |
| 495 |
. |
| B0 |
| 316 |
| 495 |
| 179 |
| 495 |
点评:问题所涉及的是生活中常见的一种现象,问题的生活化可激发学生的兴趣和求知欲望,同样这样的问题也影响学生的思维方式,学会用数学的视野关注身边的数学.

练习册系列答案
相关题目
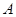 :“取出的2件产品都是二等品”的概率
:“取出的2件产品都是二等品”的概率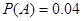
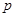 ;
;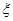 表示取出的2件产品中二等品的件数,求
表示取出的2件产品中二等品的件数,求