题目内容
8．
如图，矩形ABCD中，AB=2AD，E为边AB的中点，将△ADE沿直线DE翻折成△A1DE，若M为线段A1C的中点，则在△ADE翻折过程中，下面四个命题中不正确的是（ ）| A． | |BM|是定值 | B． | 点M在某个球面上运动 | ||
| C． | 存在某个位置，使DE⊥A1C | D． | 存在某个位置，使MB∥平面A1DE |
分析 取CD中点F，连接MF，BF，则平面MBF∥平面A1DE，可得D正确；由余弦定理可得MB2=MF2+FB2-2MF•FB•cos∠MFB，所以MB是定值，M是在以B为圆心，MB为半径的圆上，可得A，B正确．A1C在平面ABCD中的射影为AC，AC与DE不垂直，可得C不正确．
解答 解：取CD中点F，连接MF，BF，则MF∥DA1，BF∥DE，∴平面MBF∥平面A1DE，
∴MB∥平面A1DE，故D正确
由∠A1DE=∠MFB，MF=$\frac{1}{2}$A1D=定值，FB=DE=定值，
由余弦定理可得MB2=MF2+FB2-2MF•FB•cos∠MFB，所以MB是定值，故A正确．
∵B是定点，∴M是在以B为圆心，MB为半径的圆上，故B正确，
∵A1C在平面ABCD中的射影为AC，AC与DE不垂直，
∴存在某个位置，使DE⊥A1C不正确．
故选：C．
点评 掌握线面、面面平行与垂直的判定和性质定理及线面角、二面角的定义及求法是解题的关键．
练习册系列答案
相关题目
16．若复数$\frac{a+3i}{1+2i}$（α∈R，i为虚数单位）是纯虚数，则实数α的值为（ ）
| A． | -6 | B． | -4 | C． | 4 | D． | 6 |
20．抛物线y=-4x2的准线方程为（ ）
| A． | x=1 | B． | y=1 | C． | x=$\frac{1}{16}$ | D． | y=$\frac{1}{16}$ |
16．已知全集U={1，2，3，4，5}，集合A={1，2，3，5}，B={3，4}，则A∩∁UB=（ ）
| A． | {1，2，3，4} | B． | {1，2，3，5} | C． | {1，2，5} | D． | {1，2} |
15．已知变量xi，yi具有相关关系，其散点图如图所示，则它们分别对应的相关系数ri（i=1，2，3，4）的大小关系是（ ）
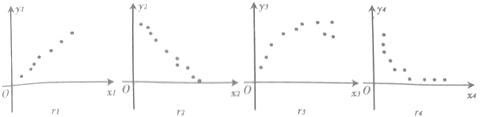
| A． | r1＞r3＞r4＞r2 | B． | r3＞r1＞r2＞r4 | C． | r3＞r1＞r4＞r2 | D． | r1＞r3＞r2＞r4 |