题目内容
设函数![]() ,其中
,其中![]() .
.
(1)若![]() ,求
,求![]() 在
在![]() 的最小值;
的最小值;
(2)如果![]() 在定义域内既有极大值又有极小值,求实数
在定义域内既有极大值又有极小值,求实数![]() 的取值范围;
的取值范围;
(3)是否存在最小的正整数![]() ,使得当
,使得当![]() 时,不等式
时,不等式![]() 恒成立.
恒成立.
解析:(1)由题意知,![]() 的定义域为
的定义域为![]() ,
,
![]() 时,由
时,由![]() ,得
,得![]() (
(![]() 舍去),
舍去),
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以当![]() 时,
时,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() 单调递增,
单调递增,
所以![]()
(2)由题意![]() 在
在![]() 有两个不等实根,
有两个不等实根,
即![]() 在
在![]() 有两个不等实根,
有两个不等实根,
设![]()
![]() ,则
,则![]() ,解之得
,解之得![]() ;
;
(3)对于函数![]() ,
,
令函数![]() ,
,
则![]() ,
,
![]()
所以函数![]() 在
在![]() 上单调递增,又
上单调递增,又![]() 时,恒有
时,恒有![]()
即![]() 恒成立.
恒成立.
取![]() ,则有
,则有![]() 恒成立.
恒成立.
显然,存在最小的正整数N=1,使得当![]() 时,不等式
时,不等式![]() 恒成立
恒成立

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
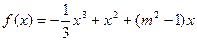 ,其中,
,其中,
 的极值和单调区间;;w
的极值和单调区间;;w ,且
,且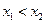 ,若对任意的
,若对任意的 ,
, 恒成立,求
恒成立,求 的取值范围
的取值范围 ,其中
,其中 ;
; 的最小正周期为
的最小正周期为 ,求
,求 ,求
,求 的值.(7分)
的值.(7分)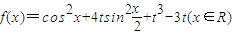 ,其中|t|<1,将f(x)的最小值记为g(t),则函数g(t)的单调递增区间为 .
,其中|t|<1,将f(x)的最小值记为g(t),则函数g(t)的单调递增区间为 . ,其中实数
,其中实数
 的单调区间;
的单调区间; 在区间
在区间 上均为增函数,求a的取值范围。
上均为增函数,求a的取值范围。 ,其中
,其中 ,
, 。
。 ,求曲线
,求曲线 在
在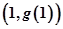 点处的切线方程;
点处的切线方程; ,使
,使 对一切正数
对一切正数 都成立?若存在,求出
都成立?若存在,求出