题目内容
已知函数![]() 是定义在
是定义在![]() 上的偶函数,当
上的偶函数,当![]() 时,
时,![]() .
.
(1)求当![]() 时
时![]() 的解析式;
的解析式;
(2)试确定函数![]() 的单调区间,并证明你的结论;
的单调区间,并证明你的结论;
(3)若![]() 且
且![]() ,证明:
,证明:![]() .
.
(1)![]()
(2)函数![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数.
上为增函数.
(3)证明见解析
解析:
(1)若![]() ,则
,则![]() , ∵函数
, ∵函数![]() 是定义在
是定义在![]() 上的偶函数,
上的偶函数,
∴ ![]() ----------3分
----------3分
(2)当![]() 时,
时,![]() . --------------6分
. --------------6分
显然当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,又
,又![]() 在
在![]() 和
和![]() 处连续,
处连续,
∴函数![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数. -----------8分
上为增函数. -----------8分
(3)∵函数![]() 在
在![]() 上为增函数,且
上为增函数,且![]() ,
,
∴当![]() 时,有
时,有![]() ,------------------10分
,------------------10分
又当![]() 时,得
时,得![]() 且
且![]() , 即
, 即![]()
∴![]() 即得
即得![]() . ----------12分
. ----------12分

练习册系列答案
相关题目
 是定义在
是定义在 上的奇函数,且
上的奇函数,且 。
。 的解析式;
的解析式; 。
。 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,
, 的解析式;
的解析式;
 是定义在
是定义在 上的以5为周期的奇函数, 若
上的以5为周期的奇函数, 若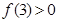 ,
, ,则a的取值范围是 ( )
,则a的取值范围是 ( )  B.
B.

 D.
D.

 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时,  (其中e是自然界对数的底,
(其中e是自然界对数的底, )
) ,求证:当
,求证:当 时,
时, ;
; 时,
时, 是定义在
是定义在 上的奇函数,且
上的奇函数,且
 的解析式;
的解析式; 的单调性;
的单调性;