题目内容
已知函数 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时,  (其中e是自然界对数的底,
(其中e是自然界对数的底, )
)
(Ⅰ)设 ,求证:当
,求证:当 时,
时, ;
;
(Ⅱ)是否存在实数a,使得当 时,
时, 的最小值是3 ?如果存在,求出实数a的值;如果不存在,请说明理由。
的最小值是3 ?如果存在,求出实数a的值;如果不存在,请说明理由。
【答案】
(Ⅰ)设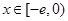 ,则
,则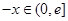 ,所以
,所以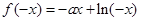
又因为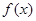 是定义在
是定义在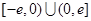 上的奇函数,所以
上的奇函数,所以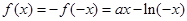
故函数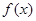 的解析式为
的解析式为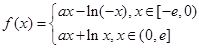 …………………3分
…………………3分
证明:当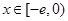 且
且
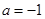 时,
时,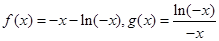 ,设
,设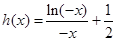
因为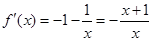 ,所以当
,所以当 时,
时,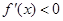 ,此时
,此时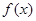 单调递减;当
单调递减;当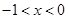 时,
时,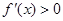 ,此时
,此时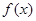 单调递增,所以
单调递增,所以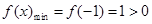
又因为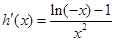 ,所以当
,所以当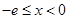 时,
时,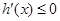 ,此时
,此时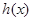 单调递减,所以
单调递减,所以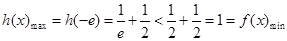
所以当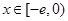 时,
时,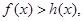 即
即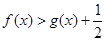 ……………………6分
……………………6分
(Ⅱ)解:假设存在实数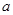 ,使得当
,使得当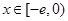 时,
时,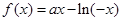 有最小值是3,则
有最小值是3,则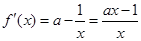
(ⅰ)当 ,
,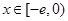 时,
时,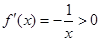 .
.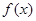 在区间
在区间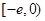 上单调递增,
上单调递增,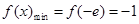 ,不满足最小值是3
,不满足最小值是3
(ⅱ)当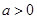 ,
,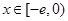 时,
时,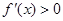 ,
,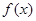 在区间
在区间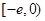 上单调递增,
上单调递增, ,也不满足最小值是3
,也不满足最小值是3
(ⅲ)当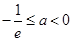 ,由于
,由于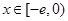 ,则
,则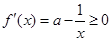 ,故函数
,故函数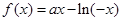 是
是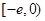 上的增函数.
上的增函数.
所以 ,解得
,解得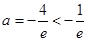 (舍去)
(舍去)
(ⅳ)当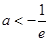 时,则
时,则
当 时,
时,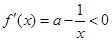 ,此时函数
,此时函数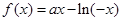 是减函数;
是减函数;
当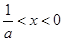 时,
时,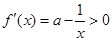 ,此时函数
,此时函数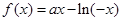 是增函数.
是增函数.
所以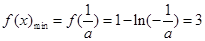 ,解得
,解得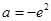
综上可知,存在实数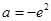 ,使得当
,使得当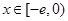 时,
时,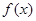 有最小值3
有最小值3
【解析】(Ⅰ)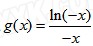 ,设
,设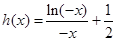 ,证明
,证明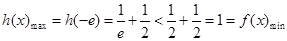 ,(Ⅱ)
,(Ⅱ)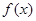 的最小值是3,讨论a的值对函数最小值的影响。
的最小值是3,讨论a的值对函数最小值的影响。

练习册系列答案
相关题目
 是定义在
是定义在 上的奇函数,且
上的奇函数,且 。
。 的解析式;
的解析式; 。
。 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,
, 的解析式;
的解析式;
 是定义在
是定义在 上的以5为周期的奇函数, 若
上的以5为周期的奇函数, 若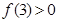 ,
, ,则a的取值范围是 ( )
,则a的取值范围是 ( )  B.
B.

 D.
D.

 是定义在
是定义在 上的奇函数,且
上的奇函数,且
 的解析式;
的解析式; 的单调性;
的单调性;