题目内容
已知a,b是两个非零向量,同时满足|a|=|b|=|a-b|,求a与a+b的夹角.解法一:根据|a|=|b|,有|a|2=|b|2,
又由|b|=|a-b|,得|b|2=|a|2-2a·b+|b|2,
∴a·b=![]() |a|2.
|a|2.
而|a+b|2=|a|2+2a·b+|b|2=3|a|2,
∴|a+b|=![]() .
.
设a与a+b的夹角为θ,则
cosθ=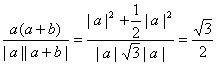 ,
,
∴θ=30°.
解法二:设向量a=(x1,y1),b=(x2,y2),
∵|a|=|b|,∴![]() .
.
由|b|=|a-b|,得x1x2+y1y2=![]() (
(![]() ),即a·b=
),即a·b=![]() (
(![]() ).
).
由|a+b|2=2(![]() )+2×
)+2×![]() (
(![]() )=3(
)=3(![]() ),得|a+b|=
),得|a+b|=![]() (
(![]() ).
).
设a与a+b的夹角为θ,则cosθ=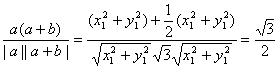 ,
,
∴θ=30°.
解法三:根据向量加法的几何意义,在平面内任取一点O,作![]() =a,OB=b,以OA、OB为邻边作平行四边形OACB.
=a,OB=b,以OA、OB为邻边作平行四边形OACB.
∵|a|=|b|,即|![]() |=|
|=|![]() |,∴OACB为菱形,OC平分∠AOB,这时
|,∴OACB为菱形,OC平分∠AOB,这时![]() =a+b,
=a+b,![]() =a-b.而|a|=|b|=|a-b|,即|
=a-b.而|a|=|b|=|a-b|,即|![]() |=|
|=|![]() |=|
|=|![]() |.
|.
∴△AOB为正三角形,则∠AOB=60°,于是∠AOC=30°,即a与a+b的夹角为30°.

练习册系列答案
相关题目