题目内容

在平面直角坐标系中，向量，已知△OFP的面积为2，且

（1）设，求向量的夹角的取值范围；

（2）设以原点O为中心，对称轴在坐标轴上，以F为右焦点的椭圆经过点M，且取最小值时，求椭圆的方程.

解（1）由

  

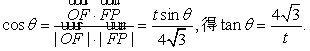
  ∴夹角的取值范围（

（2）（解法一）设P（  由（I）知：PF所在直线的倾斜角为，则

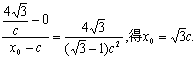    又由……9分 

∴当且仅当取最小值，此时，

∴

椭圆长轴长∴

故所求椭圆方程为

（解法二）设

 又  以下同解法一

练习册系列答案
相关题目
在平面直角坐标系xOy中，以O为极点，x正半轴为极轴建立极坐标系，曲线C的极坐标方程为：pcos(θ-
π3
)=1，M，N分别为曲线C与x轴，y轴的交点，则MN的中点P在平面直角坐标系中的坐标为
 
．
在平面直角坐标系中，A（3，0）、B（0，3）、C（cosθ，sinθ），θ∈(
π
2
，
3π
2
)，且|
AC
|=|
BC
|．
（1）求角θ的值；
（2）设α＞0，0＜β＜
π
2
，且α+β=
2
3
θ，求y=2-sin2α-cos2β的最小值．
在平面直角坐标系中，如果x与y都是整数，就称点（x，y）为整点，下列命题中正确的是
 
（写出所有正确命题的编号）．
①存在这样的直线，既不与坐标轴平行又不经过任何整点
②如果k与b都是无理数，则直线y=kx+b不经过任何整点
③直线l经过无穷多个整点，当且仅当l经过两个不同的整点
④直线y=kx+b经过无穷多个整点的充分必要条件是：k与b都是有理数
⑤存在恰经过一个整点的直线．
在平面直角坐标系中，下列函数图象关于原点对称的是（　　）
在平面直角坐标系中，以点（1，0）为圆心，r为半径作圆，依次与抛物线y2=x交于A、B、C、D四点，若AC与BD的交点F恰好为抛物线的焦点，则r=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网