题目内容
已知二次函数
有最大值且最大值为正实数，集合
，集合
（1）求
和
；
（2）定义与的差集：
且
，设
，
，x均为整数，且
，
为
取自A－B的概率，
为x取自A∩B的概率，写出
与b的三组值，使
，
，并分别写出所有满足上述条件的（从大到小）、b（从小到大）依次构成的数列{
}、{bn}的通项公式（不必证明）；
（3）若函数
中，
，
，设t1、t2是方程
的两个根，判断
是否存在最大值及最小值，若存在，求出相应的值；若不存在，请说明理由。
解：（1）∵函数
有最大值， ∴
由于
，而最大值为正数，则
，∴
∴
，
（2）要使
，
，可以使
①
中有3个元素，
中有2个元素， 
中有1个元素，
则
，
②中有6个元素，中有4个元素， 中有2个元素
则
，
③中有9个元素，中有6个元素,中有3个元素
则
，
因此，
，
（3）对于方程
，
，
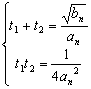
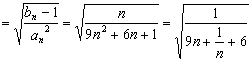
在N上单调递减
∴ 
，不存在最小值.
练习册系列答案
相关题目
已知二次函数y=f（x）的图象如图所示．