Question

 

    （理）如图，在正三棱柱（底面为正三角形，侧棱与底面垂直）ABC—A₁B₁C₁中，M、N

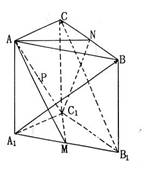
分别为A₁B₁、BC的中点.

   （I）试求的值，使；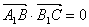

   （II）设AC₁的中点为P，在（I）的条件下，求证：NP⊥平面AC₁M.

 

 

 

（文）已知函数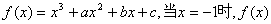的极大值

为7；当x=3时，f（x）有极小值.

（I）求函数f（x）的解析式；

（II）求函数f（x）在点P（1，f（1））处的切线方程.

 

 

 

 

 

 

Answer 1

【答案】

 （理）解：（I）以C₁点为坐标原点，C₁A₁所在直线为x轴，C₁C所在直线为z轴，建立空间直角坐标系，设A₁B₁=b，AA₁=a（）.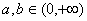

∵三棱柱ABC—A₁B₁C₁为正三棱柱，且A₁，B，B₁，C的坐标分别为A₁（b,0,0），

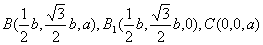. …………3分

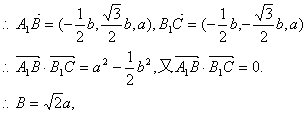
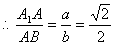            …………6分

（II）在（I）的条件下，∵A、M、N坐标分别为A（b，0，a），M，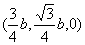

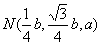，则P的坐标为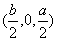.   …………8分

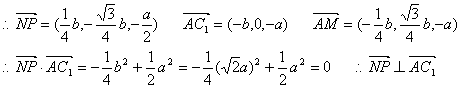
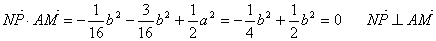
            …………10分

又AC₁与AM交于A

∴NP⊥平面AC₁M          …………12分

（文）解：（I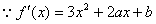）    …………2分

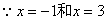    是函数的两个极点

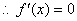    的两个根是x=－1和x=3    …………4分

   

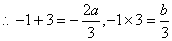
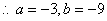             …………6分

    又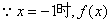的极大值为7

   

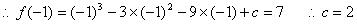
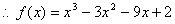           …………8分

    （II）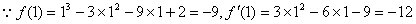

    ∴P（1，－9），过点P的切线的斜率k=－12  …………10分

    ∴过点P的切线的方程为：y+9=－12（x－1）

    即12x+y－3=0            …………12分