题目内容
(09年宣武区二模理)(13分)
如图,在正三棱柱ABC―A1B1C1中,BB1=BC=2,且M是BC的中点,点N在CC1上。
(1)试确定点N的位置,使AB1⊥MN;
(2)当AB1⊥MN时,求二面角M―AB1―N的大小。

解析:解法1:(1)连结MA、B1M,过M作MN⊥B1M,且MN交CC1点N,
|
在正△ABC中,AM⊥BC,
又∵平面ABC⊥平面BB1C1C,
平面ABC∩平面BB1C1C=BC,
∴AM⊥平面BB1C1C,
∵MN![]() 平面BB1C1C,
平面BB1C1C,
∴MN⊥AM。
∵AM∩B1M=M,
∴MN⊥平面AMB1,∴MN⊥AB1。
∵在Rt△B1BM与Rt△MCN中,
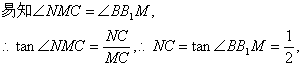
即N为C1C四等分点(靠近点C)。 ……………………6分
(2)过点M作ME⊥AB1,垂足为R,连结EN,
由(1)知MN⊥平面AMB1,
∴EN⊥AB1,
∴∠MEN为二面角M―AB1―N的平面角。
∵正三棱柱ABC―A1B1C1,BB1=BC=2,

|
解法2:(1)以点M为原点,建立如图所示的空间直角坐标系,

∴N点是C1C的四等分点(靠近点C)。 ………………6分
(2)∵AM⊥BC,平面ABC⊥平面BB1C1C,
且平面ABC∩平面BB1C1C=BC,
∴AM⊥平面BB1C1C,
∵MN![]() 平面BB1C1 C,∴AM⊥MN,
平面BB1C1 C,∴AM⊥MN,
∵MN⊥AB1,∴MN⊥平面AMB1,



练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

