题目内容
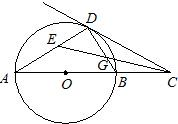
从直径AB的延长线上取一点C,过点C作该圆的切线,切点为D,若∠ACD的平分线交AD于点E,则∠CED的度数是( )
A.30°
B.45°
C.60°
D.随点C的变化而变化
【答案】分析:连OD,根据切线的性质得OD⊥CD,则∠4+∠ODC=90°,而AB为⊙O的直径,得到∠ADB=90°,得∠A+∠ABD=90°,得到∠A=∠4,又∠3=∠A+∠2,∠5=∠1+∠4,可得∠3=∠5,得到∠3= ×90°=45°.
×90°=45°.
解答:解:如图, 由切线的性质,易得∠A=∠4,
由切线的性质,易得∠A=∠4,
又∵∠3=∠A+∠2,
∠5=∠1+∠4,
而EC平分∠ACD,即∠1=∠2,
∴∠3=∠5,
∴∠3= ×90°=45°.
×90°=45°.
故选B.
点评:本题考查了切线的性质:圆心与切点的连线垂直切线;过圆心垂直于切线的直线必过切点;过圆外一点引圆的两条切线,切线长相等.也考查了直径所对的圆周角为直角以及三角形外角的性质.
 ×90°=45°.
×90°=45°.解答:解:如图,
 由切线的性质,易得∠A=∠4,
由切线的性质,易得∠A=∠4,又∵∠3=∠A+∠2,
∠5=∠1+∠4,
而EC平分∠ACD,即∠1=∠2,
∴∠3=∠5,
∴∠3=
 ×90°=45°.
×90°=45°.故选B.
点评:本题考查了切线的性质:圆心与切点的连线垂直切线;过圆心垂直于切线的直线必过切点;过圆外一点引圆的两条切线,切线长相等.也考查了直径所对的圆周角为直角以及三角形外角的性质.

练习册系列答案
相关题目
从直径AB的延长线上取一点C,过点C作该圆的切线,切点为D,若∠ACD的平分线交AD于点E,则∠CED的度数是( )
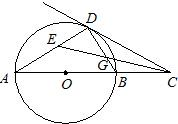

| A、30° | B、45° | C、60° | D、随点C的变化而变化 |
 (考生注意:从下列三题中任选一题,多选的只按照第一题计分)
(考生注意:从下列三题中任选一题,多选的只按照第一题计分)