题目内容
【题目】已知抛物线y2=2px(p>0)的焦点为F,过F且与x轴垂直的直线交该抛物线于A,B两点,|AB|=4.
(1)求抛物线的方程;
(2)过点F的直线l交抛物线于P,Q两点,若△OPQ的面积为4,求直线l的斜率(其中O为坐标原点).
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据抛物线的定义以及抛物线通径的性质可得![]() ,从而可得结果;(2)设直线
,从而可得结果;(2)设直线![]() 的方程为
的方程为![]() ,
,![]() 代入
代入![]() ,得
,得![]() ,利用弦长公式,结合韦达定理可得的
,利用弦长公式,结合韦达定理可得的![]() 值,由点到直线的距离公式,根据三角形面积公式可得
值,由点到直线的距离公式,根据三角形面积公式可得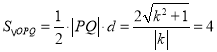 ,从而可得结果.
,从而可得结果.
(1)由抛物线的定义得![]() 到准线的距离都是p ,
到准线的距离都是p ,
所以|AB|=2p=4,
所以抛物线的方程为y2=4x.
(2)设直线l的方程为y=k(x-1),P(x1,y1),Q(x2,y2).
因为直线l与抛物线有两个交点,
所以k≠0,得![]() ,代入y2=4x,得
,代入y2=4x,得![]() ,且
,且![]() 恒成立,
恒成立,
则![]() ,y1y2=-4,
,y1y2=-4,
所以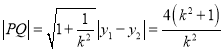 .
.
又点O到直线l的距离![]() ,
,
所以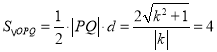 ,解得
,解得![]() ,即
,即![]() .
.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目