题目内容
已知集合A={a,b,c,d,e},B={1,2,3},定义函数f:A→B满足条件:
①函数f的值域为B;
②f(a)≠f(b),
则满足条件的不同函数f的个数
①函数f的值域为B;
②f(a)≠f(b),
则满足条件的不同函数f的个数
114
114
.分析:由分步计数原理求得故满足②的函数有3×2×3×3×3=162个,其中,不满足①函数f的值域为B 的函数有3×2×2×2×2=48个,由此求出时满足①②的函数的个数.
解答:解:根据映射的定义以及②f(a)≠f(b),可得
f(a)的值有3种方法,f(b)的值有2种方法,f(c)的值有3种方法,f(d)的值有3种方法,f(e)的值有3种方法,
故满足②的函数有3×2×3×3×3=162个.
其中,不满足①函数f的值域为B 的函数,即函数的值域中只有B={1,2,3}中的两个元素,这样的函数有3×2×2×2×2=48个.
故同时满足①②的函数有162-48=114个,
故答案为 114.
f(a)的值有3种方法,f(b)的值有2种方法,f(c)的值有3种方法,f(d)的值有3种方法,f(e)的值有3种方法,
故满足②的函数有3×2×3×3×3=162个.
其中,不满足①函数f的值域为B 的函数,即函数的值域中只有B={1,2,3}中的两个元素,这样的函数有3×2×2×2×2=48个.
故同时满足①②的函数有162-48=114个,
故答案为 114.
点评:本题主要考查映射的定义,分步计数原理的应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
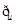 B)=R,则实数a的取值范围是 ( )
B)=R,则实数a的取值范围是 ( )