题目内容
设a,b为实数,若复数
=
,则( )
| a-bi |
| 1+2i |
| 1 |
| 1+i |
A、a=
| ||||
B、a=
| ||||
C、a=
| ||||
| D、a=1,b=-3 |
分析:直接利用复数的乘除方法化简,然后利用复数的分子分母同乘分母的共轭复数化简,利用复数的相等,求出a,b的值即可.
解答:解:复数
=
,所以a-bi=
=
=
+
i
因此a=
,b=-
.
故选A.
| a-bi |
| 1+2i |
| 1 |
| 1+i |
| 1+2i |
| 1+i |
| (1+2i)(1-i) |
| (1+i)(1-i) |
| 3 |
| 2 |
| 1 |
| 2 |
因此a=
| 3 |
| 2 |
| 1 |
| 2 |
故选A.
点评:本题是基础题,考查复数的基本运算,注意复数的化简分母实数化,复数相等的条件的应用.

练习册系列答案
相关题目
 是实数,则正整数n的最小值是4
是实数,则正整数n的最小值是4 ∈
∈
 都是非零复数,
都是非零复数,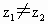 ,且复平面上O为原点,点A和B分别与
,且复平面上O为原点,点A和B分别与 和
和 对应,∠AOB=
对应,∠AOB= ,则
,则
 |≤1,则
|≤1,则 ≤arg(-zi)≤
≤arg(-zi)≤ ,其中真命题是
,其中真命题是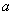

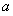
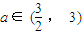 ),当n为奇数时,动点P(x、y)的轨迹为C1.当n为偶数时,动点P(x、y)的轨迹为C2.且两条曲线都经过点
),当n为奇数时,动点P(x、y)的轨迹为C1.当n为偶数时,动点P(x、y)的轨迹为C2.且两条曲线都经过点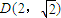 ,求轨迹C1与C2的方程;
,求轨迹C1与C2的方程;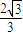 ,求实数x的取值范围.
,求实数x的取值范围.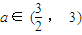 ),当n为奇数时,动点P(x、y)的轨迹为C1.当n为偶数时,动点P(x、y)的轨迹为C2.且两条曲线都经过点
),当n为奇数时,动点P(x、y)的轨迹为C1.当n为偶数时,动点P(x、y)的轨迹为C2.且两条曲线都经过点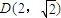 ,求轨迹C1与C2的方程;
,求轨迹C1与C2的方程;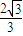 ,求实数x的取值范围.
,求实数x的取值范围.