题目内容
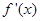 是f(x)的导函数,
是f(x)的导函数,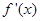 的图象如下图所示,则f(x)的图象只可能是( )
的图象如下图所示,则f(x)的图象只可能是( )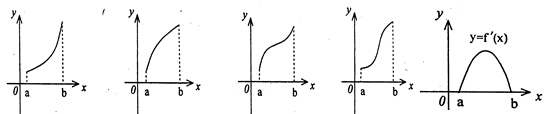
(A) (B) (C) (D)
D
解析试题分析:由图可以看出函数y=f′(x)的图象是一个二次函数的图象,
在a与b之间,导函数的值是先增大后减小
故在a与b之间,原函数图象切线的斜率是先增大后减小
因此故排除答案A,B,C.
故答案为:D.
考点:函数的单调性与导数的关系.

练习册系列答案
相关题目
函数 在
在 处有极值,则
处有极值,则 的值为( ).
的值为( ).
A. | B. | C. | D. |
设曲线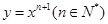 在点(1,1)处的切线与x轴的交点的横坐标为
在点(1,1)处的切线与x轴的交点的横坐标为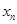 ,则
,则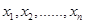 的乘积的值为( )
的乘积的值为( )
A.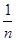 | B.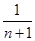 | C.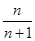 | D.1 |
函数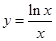 的最大值为( )
的最大值为( )
A.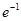 | B. | C.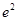 | D.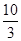 |
(2013•浙江)已知e为自然对数的底数,设函数f(x)=(ex﹣1)(x﹣1)k(k=1,2),则( )
| A.当k=1时,f(x)在x=1处取得极小值 |
| B.当k=1时,f(x)在x=1处取得极大值 |
| C.当k=2时,f(x)在x=1处取得极小值 |
| D.当k=2时,f(x)在x=1处取得极大值 |
已知e为自然对数的底数,设函数f(x)=xex,则( )
| A.1是f(x)的极小值点 |
| B.﹣1是f(x)的极小值点 |
| C.1是f(x)的极大值点 |
| D.﹣1是f(x)的极大值点 |
设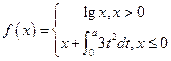 ,若f(f(1))=1,则a=( )
,若f(f(1))=1,则a=( )
| A.1 |
| B.2 |
| C.3 |
| D.4 |
函数f(x)的定义域为R,f(-1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为( )
| A.(-1,1) |
| B.(-1,+∞) |
| C.(-∞,-1) |
| D.(-∞,+∞) |
 的方向向量为
的方向向量为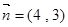 且过抛物线
且过抛物线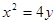 的焦点,则直线
的焦点,则直线