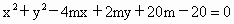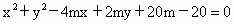题目内容
已知曲线C:![]()
(1)由曲线C上任一点E向x轴作垂线,垂足为F,点P分![]() 所成的比为
所成的比为![]() ,问:点P的轨迹可能是圆吗?请说明理由;
,问:点P的轨迹可能是圆吗?请说明理由;
(2)如果直线l的一个方向向量为![]() ,且过点M(0,-2),直线l交曲线C于A、B两点,又
,且过点M(0,-2),直线l交曲线C于A、B两点,又![]() ,求曲线C的方程.
,求曲线C的方程.
答案:
解析:
解析:
|
(1)、设 ∵点P分 ∴ 代入 当 (2)、由题设知直线l的方程为 联立方程组 ∵方程组有两解∴ 又已知 又∵ ∴曲线C的方程是 (也可以用两点间的距离公式得到 |

练习册系列答案
相关题目
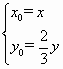
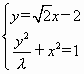 ,消去
,消去