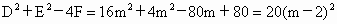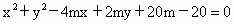题目内容
已知曲线
C：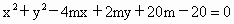
(1)
求证：不论m取何实数，曲线C恒过一定点；(2)
证明：当m≠2时，曲线C是一个圆，且圆心在一条定直线上；(3)
若曲线C与y轴相切，求m的值．
答案：略
解析：
解析：
|
解 (1)曲线C的方程可化为：
由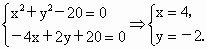 
∴不论 m取何值时，x=4，y=－2总适合曲线C的方程，即曲线C恒过定点(4，－2)．(2) 证明D=－4m，E=2m，F=20m－20，
∵  ，∴ ，∴ ，
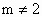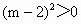∴曲线 C是一个圆，设圆心坐标为(x，y)，则由 消去m得x＋2y=0，即圆心在直线x＋2y=0上．
(3) 若曲线C与y轴相切，则m≠2，曲线C为圆，其半径 ，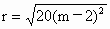
又圆心为 (2m，－m)，则 ，
∴  ． |
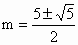练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
所成的比为
，问：点P的轨迹可能是圆吗？请说明理由；
，且过点M(0，－2)，直线l交曲线C于A、B两点，又
，求曲线C的方程．
+x2=1，由曲线C上任一点E向x轴作垂线,垂足为F,点P分
所成的比为
,问:点P的轨迹可能是圆吗?请说明理由.