题目内容
(本小题满分12分)
若函数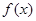 为奇函数,当
为奇函数,当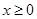 时,
时,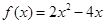 (如图).
(如图).
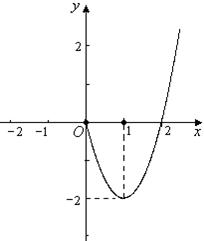
(Ⅰ)求函数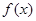 的表达式,并补齐函数
的表达式,并补齐函数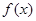 的图象;
的图象;
(Ⅱ)用定义证明:函数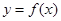 在区间
在区间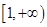 上单调递增.
上单调递增.
【答案】
(1)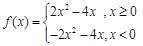 (2)利用定义法,设变量,作差,变形,定号,下结论。
(2)利用定义法,设变量,作差,变形,定号,下结论。
【解析】
试题分析:解:(Ⅰ)
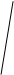 任取
任取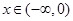 ,则
,则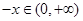 由
由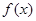 为奇函数,
为奇函数,
则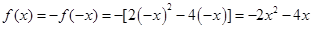 ………………………4分
………………………4分
综上所述,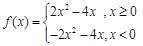 …………………………………………5分
…………………………………………5分
补齐图象。(略)…………………………………………6分
(Ⅱ)任取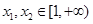 ,且
,且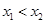 ,…………………………………7分
,…………………………………7分
则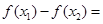
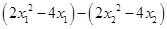 ………………………………8分
………………………………8分
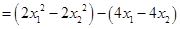
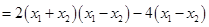
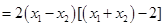 …………………………………10分
…………………………………10分
∵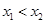 ∴
∴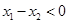
又由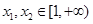 ,且
,且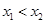 ,所以
,所以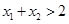 ,∴
,∴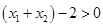
∴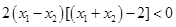 ,
,
∴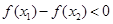 ,即
,即 ………………………………………11分
………………………………………11分
∴函数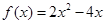 在区间
在区间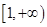 上单调递增。…………………………12分
上单调递增。…………………………12分
考点:本试题考查了奇函数的定义以及函数单调性的证明。
点评:解决该试题利用奇函数关于原点的对称性求解函数图像,同时能利用单调性的定义法证明单调性。属于基础题。

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目