Question

【题目】已知数列满足，且，点在二次函数的图象上.

（1）试判断数列是否为算术平方根递推数列？若是，请说明你的理由；

（2）记，求证：数列是等比数列，并求出通项公式；

（3）在数列中依据某种顺序从左至右取出其中的项，…，把这些项重新组成一个新数列，….若数列是首项为、公比为的无穷等比数列，且数列各项的和为，求正整数的值.

Answer 1

【答案】（1）是，理由见解析；（2）证明见解析，；（3），.

【解析】

（1）数列是算术平方根递推数列，根据题意，利用点在二次函数的图象上，可得，即可证明，从而数列是算术平方根递推数列；

（2）由，，可得，即可证明：数列是首项为，公比为的等比数列，从而求出通项公式；

（3）由题意可得数列的首项为，公比为，可得，再分类讨论，可得正整数的值.

（1）数列是算术平方根递推数列.理由如下：

∵点在函数的图象上，则.

即，而，

∴.

所以数列是算术平方根递推数列

（2）由（1）可知，，

∴，

又，

∴数列是首项为，公比的等比数列，

故数列通项公式.

（3）由题意，无穷等比数列的首项，公比（且为常数），

则无穷等比数列的各项和为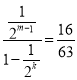，化简得.

因为且为常数，

若，则，与矛盾，

所以，

若或1时，，与矛盾，

所以，即，此时，解得，

故正整数.