题目内容
 (2012•黄冈模拟)(选做题:请在下列两题中任选一题作答,如果多做,则按所做的第一题评分)
(2012•黄冈模拟)(选做题:请在下列两题中任选一题作答,如果多做,则按所做的第一题评分)(A)如图,AB是半圆的直径,C是AB延长线一点,CD切半圆于D,CD=
| 3 |
1
1
.(B)在极坐标系中,已知圆C的圆心为(6,
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
分析:(A)连接OD,则OD⊥DC,在Rt△OED中,OE=
OB=
OD,可得∠ODE=30°.在Rt△0DC中,由∠DCO=30°、DC=
,利用直角三角形中的边角关系求出半径OD的值.
(B)设出圆上任一点的极坐标,利用两点间的距离公式表示出|PC|的长,让其值等于圆的半径5,即可得到圆C的极坐标方程,把直线方程代入圆C的方程,得到一个关于ρ的一元二次方程,利用韦达定理表示出两根之和与两根之积,表示出直线被圆截得的弦长,将两根之和与两根之积代入后,然后其值等于8,即可求出sinα的值,由α的范围,利用特殊角的三角函数值即可求出α的值.
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
(B)设出圆上任一点的极坐标,利用两点间的距离公式表示出|PC|的长,让其值等于圆的半径5,即可得到圆C的极坐标方程,把直线方程代入圆C的方程,得到一个关于ρ的一元二次方程,利用韦达定理表示出两根之和与两根之积,表示出直线被圆截得的弦长,将两根之和与两根之积代入后,然后其值等于8,即可求出sinα的值,由α的范围,利用特殊角的三角函数值即可求出α的值.
解答:解:(A)如图连接OD,则OD⊥DC,在Rt△OED中,∵E是OB的中点,ρ1-ρ2 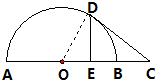
∴OE=
OB=
OD,所以∠ODE=30°.
再由△DOE∽△COD可得,在Rt△ODC中,∠DCO=30°.
∵DC=
,∴OD=DC•tan30°=
×
=1,
故答案为 1.
(B)设圆C上任一点坐标为P(ρ,θ),圆心C(6,
),圆的半径r=5,
所以|PC|=
=5,化简得:ρ2-12ρsinθ+11=0,即为圆C的极坐标方程,
把直线θ=α代入圆C的方程得:ρ2-12ρsinα+11=0.
设直线与圆交于(ρ1,α1)(ρ2,α2),根据韦达定理得:ρ1+ρ2=12sinα,ρ1ρ2=11,
所以直线被圆截得的弦长m=|ρ1-ρ2|=
=
=8,
即 (12sinα)2=64+44,化简得:sin2α=
,解得sinα=
.
又α∈[0,
],则α=
,
故答案为
.

∴OE=
| 1 |
| 2 |
| 1 |
| 2 |
再由△DOE∽△COD可得,在Rt△ODC中,∠DCO=30°.
∵DC=
| 3 |
| 3 |
| ||
| 3 |
故答案为 1.
(B)设圆C上任一点坐标为P(ρ,θ),圆心C(6,
| π |
| 2 |
所以|PC|=
ρ2+36-2ρcos(
|
把直线θ=α代入圆C的方程得:ρ2-12ρsinα+11=0.
设直线与圆交于(ρ1,α1)(ρ2,α2),根据韦达定理得:ρ1+ρ2=12sinα,ρ1ρ2=11,
所以直线被圆截得的弦长m=|ρ1-ρ2|=
| (ρ1 -ρ 2)2-4ρ 1•ρ 2 |
| (12sinα )2-44 |
即 (12sinα)2=64+44,化简得:sin2α=
| 3 |
| 4 |
| ||
| 2 |
又α∈[0,
| π |
| 2 |
| π |
| 3 |
故答案为
| π |
| 3 |
点评:本题主要考查弦切角的性质和应用,还考查了直线与圆相交的性质,两点间的距离公式,韦达定理及弦长公式,属于基础题.

练习册系列答案
相关题目
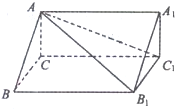 (2012•黄冈模拟)如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=
(2012•黄冈模拟)如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=