题目内容
从椭圆 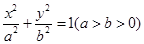 上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB//OP,
上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB//OP,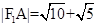 ,求椭圆的方程
,求椭圆的方程
【答案】
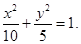
【解析】本题主要考查根据椭圆的性质求椭圆的标准方程,关键是找三个含a,b,c的等式,联立解方程组。
欲求椭圆方程,只需求出a,b的值即可,因为过点P向x轴作垂线,垂足恰为左焦点F1,所以F1O=c,由AB∥OP,可得,
△ PF1O与△BOA相似,所以PF1:F1O =BO :OA ,就此可得到一个含a,b,c的等式,因为,|F1A|= 10 + 5 ,所以a+c= 10 + 5 ,又得到一个含a,b,c的等式,再根据椭圆中,a2=b2+c2,就可解出a,b,c,得到椭圆的标准方程.
解: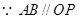
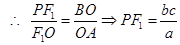 x
x
又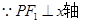
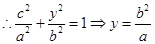
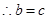
由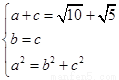 解得:
解得: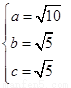
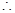 椭圆方程为
椭圆方程为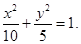

练习册系列答案
相关题目
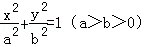 上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是( )
上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是( )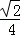 B.
B. 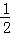 C.
C. 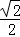 D.
D. 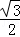
 上一点P向x轴引垂线,垂足恰为椭圆的左焦点F1,A为椭圆的右顶点,B是椭圆的上顶点,且
上一点P向x轴引垂线,垂足恰为椭圆的左焦点F1,A为椭圆的右顶点,B是椭圆的上顶点,且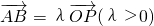 .
.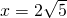 ,求椭圆方程.
,求椭圆方程.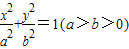 上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB∥OP(O为坐标原点),则该椭圆的离心率为( )
上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB∥OP(O为坐标原点),则该椭圆的离心率为( )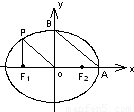

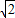

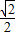
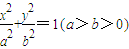 上一点P向x轴引垂线,垂足恰为椭圆的左焦点F1,A为椭圆的右顶点,B是椭圆的上顶点,且
上一点P向x轴引垂线,垂足恰为椭圆的左焦点F1,A为椭圆的右顶点,B是椭圆的上顶点,且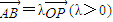 .
.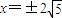 ,求椭圆方程.
,求椭圆方程.