题目内容
已知直线过点(1,1),且在两个坐标轴上的截距相等,则该直线的方程为 .
【答案】分析:直线过点(1,1),且在两个坐标轴上的截距相等,可设出直线l的点斜式方程,利用截距相等列式相等解之即可.
解答:解:∵直线l过点(1,1),且在两个坐标轴上的截距相等,
∴直线l的斜率存在且不为0,设为k,则k≠0,
∴直线l的方程为:y-1=k(x-1),
令x=0,y=1-k;
令y=0,x=1-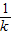 ,
,
依题意,1-k=1-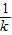 ,
,
∴k2=1,
∴k=±1.
∴该直线的方程为y=x或y=2-x.
故答案为:y=x或y=2-x.
点评:本题考查直线的截距式方程,考查分类讨论思想与运算能力,属于基础题.
解答:解:∵直线l过点(1,1),且在两个坐标轴上的截距相等,
∴直线l的斜率存在且不为0,设为k,则k≠0,
∴直线l的方程为:y-1=k(x-1),
令x=0,y=1-k;
令y=0,x=1-
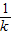 ,
,依题意,1-k=1-
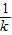 ,
,∴k2=1,
∴k=±1.
∴该直线的方程为y=x或y=2-x.
故答案为:y=x或y=2-x.
点评:本题考查直线的截距式方程,考查分类讨论思想与运算能力,属于基础题.

练习册系列答案
相关题目