题目内容
【题目】在四面体ABCD中，若AB=CD= 
，AC=BD=2，AD=BC= 
，则直线AB与CD所成角的余弦值为（ ）
A.﹣ 
B.﹣ 
C.
D.
【答案】D
【解析】解：如图所示，构造长方体，设长方体的长、宽、高分别为a，b，c，则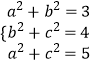 
，∴a= 
，b=1，c= 
，
即CE=1，CF= ，FB= ，
∵EF∥AB，
∴∠FOC为直线AB与CD所成角，
△OCF中，OC=OF= 
，CF= ，∴cos∠FOC=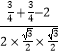 
= 
，
故选D．
【考点精析】通过灵活运用异面直线及其所成的角，掌握异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系即可以解答此题．
练习册系列答案
阅读快车系列答案
相关题目
【题目】某制造商
月生产了一批乒乓球，随机抽样
个进行检查，测得每个球的直径(单位：mm)，将数据分组如下表
分组 | 频数 | 频率 |
| 10 | |
| 20 | |
| 50 | |
| 20 | |
合计 | 100 |
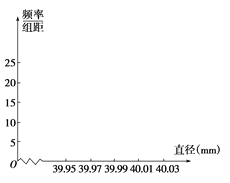
(1)请在上表中补充完成频率分布表(结果保留两位小数)，并在上图中画出频率分布直方图；
(2)统计方法中，同一组数据常用该组区间的中点值(例如区间
的中点值是
)作为代表.据此估计这批乒乓球直径的平均值(结果保留两位小数).
